Cho mặt cầu có phương trình x 2 + y 2 + z 2 - 4 x - 2 y + 2 z + 5 = 0 và mặt phẳng P : 3 x - 2 y + 6 z + m = 0 . S và P giao nhau khi
A. 2 ≤ m ≤ 3
B. m > 2 hoặc m < 2
C. - 5 ≤ m ≤ 9
D. m > 9 hoặc m < - 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 11 2018
Đáp án A
Mặt cầu (S) có tâm I(-1;4;-3) và có bán kính R = 6. Gọi H là hình chiếu vuông góc của I trên trục Ox. Ta có H(-1;0;0) và IH=5.
Gọi K là hình chiếu vuông góc của I trên mặt phẳng (P). Ta có
d(I; (P)) = IK ≤ IH = 5 < R = 6
Do đó mặt phẳng (P) luôn cắt mặt cầu (S) theo một đường tròn. Vậy không tồn tại mặt phẳng (P) chứa Ox và tiếp xúc với (S)
CM
7 tháng 12 2017
Đáp án B.
Gọi 
thuộc
d
1
và 
thuộc d 2 là 2 giao điểm.
Ta có: 
Vì M N → cùng phương với
nên ta có:
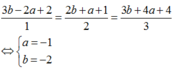
điểm này thuộc đường thẳng ở đáp án B.
Đáp án C