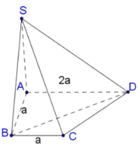
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B , AD = 2 a , AB = BC = a , SA vuông góc với đáy, SB tạo với đáy một góc 30 o . Tính tỉ số thể tích V SABD V SBCD ?
A. 1 2
B. 3
C. 1 4
D. 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Phương pháp
+ Xác định góc giữa đường thẳng d và mặt phẳng (P) là góc giữa đường thẳng d và đường thẳng d' với d' là hình chiếu của d trên mặt phẳng (P).
+ Thể tích hình chóp có chiều cao h và diện tích đáy S là V = 1 3 h S
Cách giải:
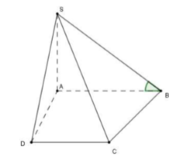
+ Ta có SA ⊥ (ABCD) => AB là hình chiếu của
SB lên mặt phẳng (ABCD) . Suy ra góc giữa SB và đáy là góc ∠ SBA = 600.
+ Xét tam giác vuông SAB có: ![]()
+ Diện tích đáy
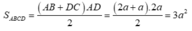
+ Thể tích khối chóp là
![]()
Chọn C.

Đáp án C
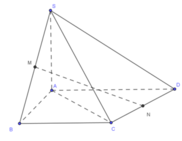
Kẻ CN
⊥
AB ta dễ dàng tính được ![]()
![]()
=> tam giác ADC vuông tại C. Từ đó NC ⊥ (SAC)
Gọi O là trung điểm của AC, dễ dàng cm được BD ⊥ (SAC)
=> MK ⊥ (SAC). vơí K là trung điểm của SO, từ đó KC là hc của MN lên .
Ta kẻ KZ ⊥ AC
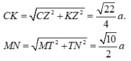
với T là trung điểm của AB.
Gọi α là góc tạo với MN và (SAC)
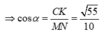

Đáp án A
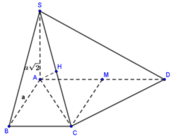
Gọi M là trung điểm AD, khi đó CM = MA = MD nên tam giác ACD vuông tại C.
