Cho tam giác ABC vuông tại A Kẻ AH vuông góc BC(H thuộc BC) Tia phân giác góc HAC cắt BC ở D.CMR Tam giác ABD cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CU
17 tháng 2 2019
chị tự kẻ hình :
AH _|_ BC (gt) => góc DHA = 90o (đn)
=> góc ADH + góc DHA + góc DAH = 180 (đl)
=> góc ADH + 90 + góc DAH = 180
=> góc ADH = 180 - 90 - góc DAH
=> góc ADH = 90 - góc DAH (1)
có tam giác ABC vuông tại A (gt)
=> góc DAB + góc CAD = 90
=> góc DAB = 90 - góc CAD (2)
AD là phân giác của góc HAC (gt) => góc CAD = góc DAH (đn) (3)
(1)(2)(3) => góc DAB = góc ADB
=> tam giác ABD cân tại B (dh)
17 tháng 2 2019
Ta có: \(\widehat{CAD}=\widehat{BAC}-\widehat{BAD}=90^0-\widehat{BAD}\)
\(\widehat{HAD}=90^0-\widehat{BDA}\)
Mà \(\widehat{CAD}=\widehat{HAD}\) (vì AD là tia phân giác của góc HAC)
Do đó: \(\widehat{BAD}=\widehat{BDA}\Rightarrow\Delta ABD\) cân tại B
Chúc bạn học tốt.
TQ
4
29 tháng 1 2021
Đáp án:
ta có: góc BAD + góc DAC = 90 độ
góc ADH + góc HAD = 90 độ ( vì tam giác AHD vuông tại H )
mà DAC = HAD ( AD là tia phân giác)
suy ra góc BAD = góc BDA
vậy tam giác ABD là tam giác cân tại B
ta có : góc CAE + góc EAB = 90 độ
góc CEA + góc HAE = 90 độ (tam giác AEH vuông tại H)
mà EAB=HAE suy ra góc CAE = góc CEA
vậy tam giác ACE cân tại C
- Ta có : AB=BD ( tam giác ABD cân)
AC=CE( tam giác AEC cân )
suy ra AB+AC=BD+CE
=BE+ED+CD+ED
=BC+DE
29 tháng 1 2021
Xét t/g AHD vuông tại H có
ˆHAD+ˆBDA=90oHAD^+BDA^=90o (t/c)
=> ˆDAC+ˆBDA=90oDAC^+BDA^=90o
Mà ˆDAC+ˆDAB=ˆBAC=90oDAC^+DAB^=BAC^=90o
=> ˆBAD=ˆBDABAD^=BDA^
=> t/g ABD cân tại B
AH
Akai Haruma
Giáo viên
6 tháng 1
Lời giải:
Ta có: $\widehat{BAE}=\widehat{BAC}-\widehat{EAC}$
$=90^0-\frac{1}{2}\widehat{HAC}(1)$
$\widehat{AEB}=\widehat{EAC}+\widehat{ECA}$
$=\frac{1}{2}\widehat{HAC}+(90^0-\widehat{HAC})$
$=90^0-\frac{1}{2}\widehat{HAC}(2)$
Từ $(1); (2)\Rightarrow \widehat{BAE}=\widehat{AEB}$
$\Rightarrow \triangle ABE$ cân tại $B$
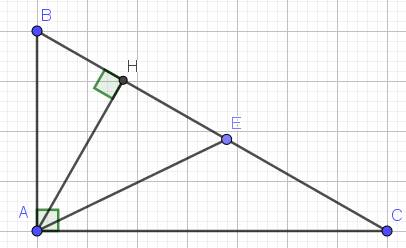
Ta có Góc BDA + Góc HAD = 90 độ ( 1 )
Lại có Góc BAD + Góc DAC = 90 độ ( 2 )
Mà AD là tia phân giác của góc HAC
->Góc HAD = Góc DAC ( 3 )
Từ ( 1 ) ( 2 ) ( 3 )
->Góc BAD = Góc BDA
Xét tam giác ABD có
Góc BAD = Góc BDA
-> Tam giác ABD là tâm giác cân tại B