Cho lăng trụ đứng ABC.A′B′C′ có đáy là tam giác cân, AB = AC = 2 a , BAC ^ = 120 ° . Mặt phẳng AB ' C ' tạo với đáy một góc 60 ° . Thể tích khối lăng trụ bằng
A. a 3 2 (dvtt)
B. a 3 (dvtt)
C. a 3 6 (dvtt)
D. 3 a 3 (dvtt)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Gọi I là trung điểm của B′C′.Trong tam giác A′B′C′
ta có

![]()

Đáp án B
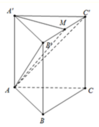
Ta có: S A B C = 1 2 A B . A C . sin A = a 2 3 4
Gọi M là trung điểm của B ' C ' khi đó
B ' C ' ⊥ A ' M B ' C ' ⊥ A A ' ⇒ B ' C ' ⊥ A ' M A
Suy ra A ' M A ⏜ = A B ' C ' ' A ' B ' C ' ⏜ = 30 °
Lại có A ' M = A ' B sin 30 ° = a 2 ⇒ A A ' = A ' M t a n 30 ° = a 2 3
⇒ V A B C . A ' B ' C ' = S A B C . A A ' = a 3 8

Đáp án A
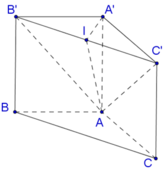
Gọi I là trung điểm của B′C′.
Trong tam giác A′B′C′ ta có
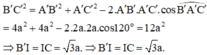
Trong tam giác A′B′I ta có
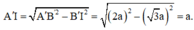


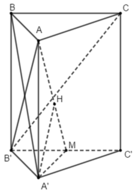
+ Gọi M là trung điểm của B’C’
Tam giác AB’C’ cân tại A ⇒ AM ⊥ B’C’
Tam giác A’B’C’ cân tại A’ ⇒ A’M ⊥ B’C’
Mà (AB’C’) ∩ (A’B’C’) = B’C’
Do đó góc giữa hai mặt phẳng (AB’C’) và (A’B’C’) là góc giữa 2 đường thẳng AM và A’M và chính là góc AMA’ ⇒ A M A ' ^ = 60 °
Ta có: A’M = 1/2 A’C’ = a/2 ⇒ AA’ = A’M. tan 60 ° = a 3 2
+ Ta có BC // (AB’C’) ⇒ d(BC; (AB’C’)) = d(B; (AB’C’))
Ta chứng minh được d(B; (AB’C’)) = d(A’; (AB’C’))
Do đó: d(BC; (AB’C’)) = d(A’; (AB’C’))
+ Ta chứng minh được (AA’M) ⊥ (AB’C’), trong mặt phẳng (AA’M), dựng A’H ⊥ AM tại H
⇒ A’H ⊥ (AB’C’) ⇒ d(A’; (AB’C’)) = A’H ⇒ d(BC; (AB’C’)) = A’H
+ Tính A’H
Ta có: 1 A ' H 2 = 1 A A ' 2 + 1 A ' M 2 ⇒ A’H = a 3 4
Vậy d(BC; (AB’C’)) = a 3 4 .
Đáp án B