Cho tam giác ABC đều Trên cạnh AB BC AC lần lượt lấy các điểm D,E,F sao cho AD=BE=CF.CMR:Tam giác DEF đều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


vì AD=BE=CF nên AD,BE,CF là đường cao là trung trực là tung tuyến phân giác mà 3 đường cao đi qua 1 điểm , điểm này cách đều D,E,F nên tam giác DEF là tam giac đều

Xét ΔABCΔABC là tam giác đều (gt)
=> {ABCˆ=ACBˆ=BACˆAB=AC=BC{ABC^=ACB^=BAC^AB=AC=BC (tính chất tam giác đều)
Có : ⎧⎩⎨⎪⎪D∈ABE∈BCF∈AC{D∈ABE∈BCF∈AC (gt)
=> ⎧⎩⎨⎪⎪AB=AD+BDAC=CF+CFBC=BE+CE{AB=AD+BDAC=CF+CFBC=BE+CE
Mà : {AD=BE=CFAB=AC=BC{AD=BE=CFAB=AC=BC (cmt)
=> BD=AF=CEBD=AF=CE
Xét ΔADF;ΔBEDΔADF;ΔBED có :
AF=BD(cmt)AF=BD(cmt)
DAFˆ=EBDˆDAF^=EBD^ (gt)
AD=BE(cmt)AD=BE(cmt)
=> ΔADF=ΔBED(c.g.c)ΔADF=ΔBED(c.g.c)
=> DF=DEDF=DE (2 cạnh tương ứng) (1)
Xét ΔADF;ΔCEFΔADF;ΔCEF có :
AF=EC(cmt)AF=EC(cmt)
DAFˆ=FCEˆDAF^=FCE^ (tam giác ABC đều - gt)
DA=FC(cmt)DA=FC(cmt)
=> ΔADF=ΔCEF(c.g.c)ΔADF=ΔCEF(c.g.c)
=> DF=EFDF=EF ( 2 cạnh tương ứng) (2)
- Từ (1) và (2) => DF=DE=EFDF=DE=EF
Xét ΔDEFΔDEF có :
DF=DE=EFDF=DE=EF (cmt)
=> ΔDEFΔDEF là tam giác đều (đpcm)

Tam giác ABC đều
=> Góc A=Góc B=Góc C
Chứng minh Tam giác ADE và Tam giác BED:
AD=BE
Góc A=Góc B
AF=BD
=> Tam giác ADE=Tam giác EBD(c.g.c) (1)
=>DF=ED (3)
Tương tự chứng minh Tam giác ECF=Tam giác FAD(c.g.c) (2)
EF=DF (4)
Từ (1) và (2) =>Tam giác BED=Tam giác CFE
=>ED=FE (5)
Từ (3);(4);(5) => DF=DE=FE
=> Tam giác DEF là tam giác đều

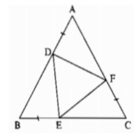
Ta có: AB = AD +DB (1)
BC = BE + EC (2)
AC = AF + FC (3)
AB = AC = BC ( vì tam giác ABC là tam giác đều) (4)
AD = BE = CF ( giả thiết) (5)
Từ (1), (2), (3) và (4),(5) suy ra: BD = EC = AF
Xét ΔADF và ΔBED, ta có:
AD = BE (gt)
∠A =∠B =60o (vì tam giác ABC đều)
AF = BD (chứng minh trên)
suy ra: ΔADF= ΔBED (c.g.c)
⇒ DF=ED (hai cạnh tương ứng) (6)
Xét ΔADF và ΔCFE, ta có:
AD = CF (gt)
∠A =∠C =60o (vì tam giác ABC đều)
AF = CE (chứng minh trên)
suy ra: ΔADF= ΔCFE (c.g.c)
Nên: DF = FE (hai cạnh tương ứng) (7)
Từ (6) và (7) suy ra: DF = ED = FE
Vậy tam giác DFE đều

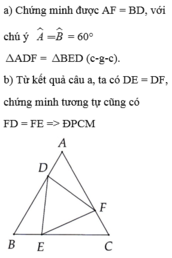
chtt nha huyền trần thị thanh