Điều kiện nào dưới đây là điều kiện cần và đủ để điểm O là trung điểm của đoạn AB.
A.OA= OB
B. O A → = O B →
C. A O → = B O →
D. O A → + O B → = 0 →
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Điểm O là trung điểm của đoạn AB khi và chỉ khi OA= OB và ![]() là ngược hướng.
là ngược hướng.
Vậy ![]() .
.

Điểm O là trung điểm của đoạn thẳng AB khi và chỉ khi OA = OB và O nằm giữa A; B.
Khi đó, hai vecto O A → ; O B → ngược hướng và có độ dài bằng nhau nên O A → = − O B →
Đáp án D

Tham khảo:
a) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) ngược hướng

\( \Leftrightarrow \left\{ \begin{array}{l}AB//AM\\B \; \text {và}\; M \; \text {nằm cùng phía so với điểm A}\end{array} \right.\)
\( \Leftrightarrow \) A, B, thẳng hàng và A nằm giữa B và M
b) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) cùng phương
TH1: \(MA < MB\)
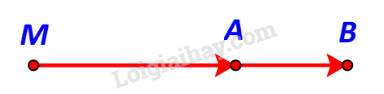
M, A, B thẳng hàng & A nằm giữa M và B.
TH2: \(MA > MB\)
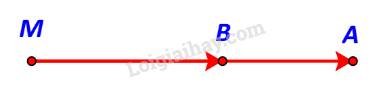
M, A, B thẳng hàng & B nằm giữa M và A.
c) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) cùng hướng
TH1: \(AM < AB\)

A, M, B thẳng hàng & M nằm giữa A và B.
TH2: \(AB < AM\)

A, M, B thẳng hàng & B nằm giữa A và M.
d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng

\( \Leftrightarrow \left\{ \begin{array}{l}MA//MB\\A \; \text {và} \; B\; \text {nằm về hai phía so với điểm M}\end{array} \right.\)
\( \Leftrightarrow \) A, M, B thẳng hàng & M nằm giữa A và B.
Vậy điều kiện cần và đủ để M nằm giữa A và B là d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng

Ta có
(1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là B A → = - 2 A C →
(3) Điều kiện cần và đủ để M là trung điểm của đoạn PQ là P Q → = 2 P M →
Phát biểu sai: (2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là
Do đó câu (1) và câu (3) là đúng.
Chọn A.

Chọn A.
Ta có:
(1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là ![]()
(3) Điều kiện cần và đủ để M là trung điểm của đoạn PQ là ![]()
Phát biểu sai: (2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là ![]()
Do đó câu (1) và câu (3) là đúng.

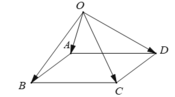
+) Trước hết, điều kiện cần và đủ để tứ giác ABCD là hình bình hành là: 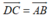 .
.
+) Với mọi điểm O bất kì khác A, B, C, D ta có:
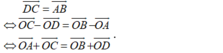
- Vậy điều kiện cần và đủ để tứ giác ABCD là hình bình hành là:
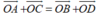

Gọi M là trung điểm của AB
Xét ΔOAB có OM là đường trung tuyến
nên \(\overrightarrow{OA}+\overrightarrow{OB}=2\cdot\overrightarrow{OM}\)
=>Giá của vecto OA+vecto OB là đường thẳng OM
Để OM là phân giác của góc AOB thì OM vừa là đường trung tuyến vừa là đường phân giác của ΔOAB
=>ΔOAB cân tại O
=>OA=OB

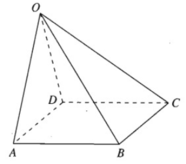
Giả sử bốn điểm A, B, C, D tạo thành một hình bình hành ta có:
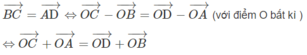
Ngược lại, giả sử ta có hệ thức:
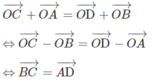
Vì A, B, C, D không thẳng hàng nên tứ giác ABCD là hình bình hành.
Điểm O là trung điểm của đoạn AB khi và chỉ khi OA= OB và là ngược hướng.Vậy
O A → + O B → = 0 →