Viết một số A bất kì có 3 chữ số, viết tiếp ba chữ số đó một lần nữa, được số B có 6 chữ số. Chia số B cho 7, rồi chia thương tìm được cho 11, sau đó lại chia thương tìm được cho 13. Kết quả được số A, hãy giải thích tại sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
4 tháng 12 2017
Đúng(0)
Những câu hỏi liên quan
LN
10 tháng 10 2017
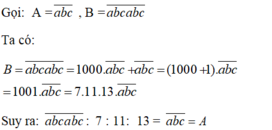
Mình có cách phân tích khác nhé : 
Gọi A là \(\overline{abc}\) thì ta được : B = \(\overline{abc}.1000+\overline{abc}\)
Theo bài ra ta có :
\(\left(\overline{abc}.1000+\overline{abc}\right):7:11:13=\overline{abc}\)
\(\overline{abc}\left(1000+1\right)=\overline{abc}.7.11.13\)
\(\overline{abc}.1001=\overline{abc}.1001\)
TP
20 tháng 5 2017
(A=overline{abc}), (B=overline{abcabc}).Ta có:
(overline{abc}).7.11.13=(overline{abc}).1001=(overline{abcabc}) nên
(overline{abcabc}):7:11:13=(overline{abc})
B
8 tháng 9 2017
Giả sử A là abc¯abc¯
=> B=abcabc¯B=abcabc¯
Ta có
abc¯.1001=abcabc¯abc¯.1001=abcabc¯
=> abc¯=abcabc¯:1001abc¯=abcabc¯:1001 (1)
Mặt khác
Giải giả thiết ta được
abcabc¯:7:11:13=abc¯abcabc¯:7:11:13=abc¯
=> abcabc¯:(7.11.13)=abc¯abcabc¯:(7.11.13)=abc¯
=> abcabc¯:1001=abc¯abcabc¯:1001=abc¯
15 tháng 8 2015
Gọi A là abc thì B=abc.1000+abc
Theo đề bài ta có
(abc.1000+abc):7:11:13=abc
abc(1000+1)=abc.1001
abc(1000+1)=abc.1001
Vậy đó mình giải thích xong rồi suy ra B:7:11:13=A
CC
21 tháng 9 2016
Gọi số A là abc. Khi đó số B là abcabc.
Phân tích B=abcabc=abc000+abc=abc.1000+abc=abc.1001=abc.7.11.13.
Bây giờ chia B cho 7,11,13 thì sẽ được A thôi!
BD
21 tháng 9 2016
Viết một số A bất kì có 3 chữ số , viết tiếp 3 chữ số đó một lần nữa , được số B có 6 chữ số . Chia số B cho 7 , rồi chia thương tìm được cho 11 , sau đó lại chia thương tìm được cho 13 . Kết quả được số A , hãy giải thích vì sao ?
Gọi số A là abc. Khi đó số B là abcabc.
Phân tích B=abcabc=abc000+abc=abc.1000+abc=abc.1001=abc.7.11.13.
Bây giờ chia B cho 7,11,13 thì sẽ được A thôi!