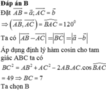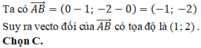Cho hai vec tơ a→ và b→ có a → = 3 , b → = 3 , a → , b → = 120 ° . Với giá trị nào của m thì hai vec tơ a → + m b → v à a → - m b → vuông góc với nhau?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

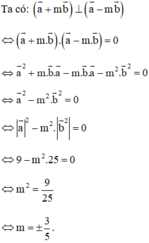

a) Đúng
Giải thích: Nhận thấy a→ = -3.i→
Vì –3 < 0 nên a→ và i→ ngược hướng.
b) Đúng.
Giải thích:
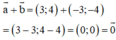
⇒ a→ = -b→ nên a→ và b→ là hai vec tơ đối nhau.
c) Sai
Giải thích:
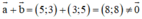
⇒ a→ ≠ -b→ nên a→ và b→ không phải là hai vec tơ đối nhau.
d) Đúng
Nhận xét SGK : Hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.

Đáp án B
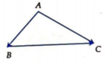
Cách 1:
Đặt A B → = a → ; A C → = b → ⇒ A B → , A C → = B A C ^ = 120 0
Ta có A B → − A C → = B C → = a → − b →
Áp dụng định lý hàm cosin cho tam giác ABC ta có
B C 2 = A B 2 + A C 2 − 2 A B . A C . cos B A C ^ = 49 ⇒ B C = 7
Ta chọn B
Cách 2:
a → − b → 2 = a → 2 + b → 2 − 2 a → b → = a → 2 + b → 2 − 2 a → b → cos a → , b → = 3 2 + 5 2 − 2.3.5. − 1 2 = 49
⇒ a → − b → 2 = 49 ⇒ a → − b → = 7
Ta chọn B