Cho hình tam giác ABC có góc đỉnh A là góc vuông. Qua đỉnh A hãy vẽ đường thẳng AX song song với cạnh BC, qua đỉnh C, hãy vẽ đường thẳng CY song song với cạnh AB. Hai đường thẳng AX và CY cắt nhau tại điểm D, nêu tên các cặp cạnh song song với nhau có trong hình tứ giác ADCB


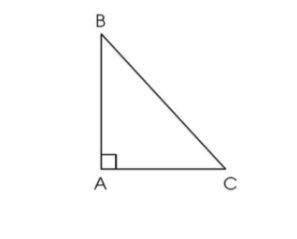
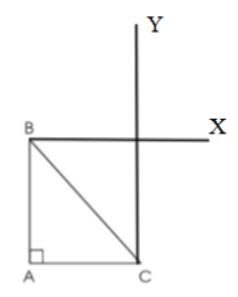
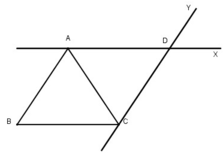
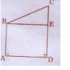
Dùng ê ke để vẽ, ta được tứ giác ADBC như sau:
Trong tứ giác ADBC có:
- Cặp cạnh AD và BC song song với nhau
- Cặp cạnh AB và DC song song với nhau.