Chứng minh các đẳng thức sau với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b)
Với n = 1.
\(VT=B_n=1;VP=\dfrac{1\left(1+1\right)\left(1+2\right)}{6}=1\).
Vậy với n = 1 điều cần chứng minh đúng.
Giả sử nó đúng với n = k.
Nghĩa là: \(B_k=\dfrac{k\left(k+1\right)\left(k+2\right)}{6}\).
Ta sẽ chứng minh nó đúng với \(n=k+1\).
Nghĩa là:
\(B_{k+1}=\dfrac{\left(k+1\right)\left(k+1+1\right)\left(k+1+2\right)}{6}\)\(=\dfrac{\left(k+1\right)\left(k+2\right)\left(k+3\right)}{6}\).
Thật vậy:
\(B_{k+1}=B_k+\dfrac{\left(k+1\right)\left(k+2\right)}{2}\)\(=\dfrac{k\left(k+1\right)\left(k+2\right)}{6}+\dfrac{\left(k+1\right)\left(k+2\right)}{2}\)\(=\dfrac{\left(k+1\right)\left(k+2\right)\left(k+3\right)}{6}\).
Vậy điều cần chứng minh đúng với mọi n.
c)
Với \(n=1\)
\(VT=S_n=sinx\); \(VP=\dfrac{sin\dfrac{x}{2}sin\dfrac{2}{2}x}{sin\dfrac{x}{2}}=sinx\)
Vậy điều cần chứng minh đúng với \(n=1\).
Giả sử điều cần chứng minh đúng với \(n=k\).
Nghĩa là: \(S_k=\dfrac{sin\dfrac{kx}{2}sin\dfrac{\left(k+1\right)x}{2}}{sin\dfrac{x}{2}}\).
Ta cần chứng minh nó đúng với \(n=k+1\):
Nghĩa là: \(S_{k+1}=\dfrac{sin\dfrac{\left(k+1\right)x}{2}sin\dfrac{\left(k+2\right)x}{2}}{sin\dfrac{x}{2}}\).
Thật vậy từ giả thiết quy nạp ta có:
\(S_{k+1}-S_k\)\(=\dfrac{sin\dfrac{\left(k+1\right)x}{2}sin\dfrac{\left(k+2\right)x}{2}}{sin\dfrac{x}{2}}-\dfrac{sin\dfrac{kx}{2}sin\dfrac{\left(k+1\right)x}{2}}{sin\dfrac{x}{2}}\)
\(=\dfrac{sin\dfrac{\left(k+1\right)x}{2}}{sin\dfrac{x}{2}}.\left[sin\dfrac{\left(k+2\right)x}{2}-sin\dfrac{kx}{2}\right]\)
\(=\dfrac{sin\dfrac{\left(k+1\right)x}{2}}{sin\dfrac{x}{2}}.2cos\dfrac{\left(k+1\right)x}{2}sim\dfrac{x}{2}\)\(=2sin\dfrac{\left(k+1\right)x}{2}cos\dfrac{\left(k+1\right)x}{2}=2sin\left(k+1\right)x\).
Vì vậy \(S_{k+1}=S_k+sin\left(k+1\right)x\).
Vậy điều cần chứng minh đúng với mọi n.

\(tan^2x-sin^2x=tan^2x.sin^2x\)
\(\Leftrightarrow\dfrac{sin^2x}{cos^2x}-sin^2x=\dfrac{sin^2x}{cos^2x}.sin^2x\)
\(\Leftrightarrow\dfrac{sin^2x\left(1-cos^2x\right)}{cos^2x}=\dfrac{sin^4x}{cos^2x}\)
\(\Leftrightarrow\dfrac{sin^2x.sin^2x}{cos^2x}=\dfrac{sin^4x}{cos^2x}\)
\(\Rightarrowđpcm\)

\(a)\;sin(\alpha + \beta ).sin(\alpha - \beta ) = \;\frac{1}{2}.\left[ {cos\left( {\alpha + \beta - \alpha + \beta } \right) - cos\left( {\alpha + \beta + \alpha - \beta } \right)} \right]\)
\(\begin{array}{l} = \;\frac{1}{2}.(cos2\beta - cos2\alpha ) = \;\frac{1}{2}.(1 - 2si{n^2}\beta - 1 + 2si{n^2}\alpha )\\ = si{n^2}\alpha - si{n^2}\beta \end{array}\)
\(\begin{array}{l}b)\;co{s^4}\alpha - co{s^4}\left( {\alpha - \frac{\pi }{2}} \right) = \;co{s^4}\alpha - si{n^4}\alpha \\ = \;(co{s^2}\alpha + si{n^2}\alpha )(co{s^2}\alpha - si{n^2}\alpha )\\ = \;co{s^2}\alpha -si{n^2}\alpha = cos2\alpha .\end{array}\)

Có \(\sin^2x+\cos^2x=1\Rightarrow2\sin^2x=1-\cos^2x+\sin^2x\)
\(\Rightarrow1+\sin^2x=2\sin^2x+\cos^2x\)
\(\Rightarrow VT=\frac{2\sin^2x+\cos^2x}{\cos^2x}=2\tan^2x+1\)

\(VP=\frac{2\sin^2x-1}{\sin^4x}=\frac{\sin^2x+\sin^2x-1}{\sin^4x}=\frac{\sin^2x-\cos^2x}{\sin^4x}\)
\(=\frac{\left(\sin^2x-\cos^2x\right).1}{\sin^4x}=\frac{\left(\sin^2x-\cos^2x\right)\left(\sin^2x+\cos^2x\right)}{\sin^4x}=\frac{\sin^4x-\cos^4x}{\sin^4x}\)
\(=1-\cot^4x\)=VT

\(a)sin^4x+cos^4x=1-2sin^2x\cdot cos^2x\)
\(\Leftrightarrow sin^4x+2sin^2x\cdot cos^2x+cos^4x=1\)
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2=1\)(luôn đúng)
a) \sin ^{4} x+\cos ^{4} x=\sin ^{4} x+\cos ^{4} x+2 \sin ^{2} x \cos ^{2} x-2 \sin ^{2} x \cos ^{2} xsin4x+cos4x=sin4x+cos4x+2sin2xcos2x−2sin2xcos2x
\begin{aligned}&=\left(\sin ^{2} x+\cos ^{2} x\right)^{2}-2 \sin ^{2} x \cos ^{2} x \\&=1-2 \sin ^{2} x \cos ^{2} x\end{aligned}=(sin2x+cos2x)2−2sin2xcos2x=1−2sin2xcos2x
b) \dfrac{1+\cot x}{1-\cot x}=\dfrac{1+\dfrac{1}{\tan x}}{1-\dfrac{1}{\tan x}}=\dfrac{\dfrac{\tan x+1}{\tan x}}{\dfrac{\tan x-1}{\tan x}}=\dfrac{\tan x+1}{\tan x-1}1−cotx1+cotx=1−tanx11+

a) Ta có: \(1-\frac{\sin^2x}{1+\cot x}-\frac{\cos^2x}{1+\tan x}=1-\frac{\sin^2x}{1+\frac{\cos x}{\sin x}}-\frac{\cos^2x}{1+\frac{\sin x}{\cos x}}\) (Đk: sinx và cosx khác 0)
\(=1-\frac{\sin^3x}{\sin x+\cos x}-\frac{\cos^3x}{\cos x+\sin x}\)
\(=1-\frac{\left(\sin x+\cos x\right)\left(\sin^2x-\sin x.\cos x+\cos^2x\right)}{\sin x+\cos x}\)
\(=1-\left(\sin^2x+\cos^2x-\sin x.\cos x\right)\) (do sinx + cosx luôn khác 0)
\(=\sin x.\cos x\) ( do \(\sin^2x+\cos^2x=1\))
b) Ta có: \(\frac{\sin^2x+2\cos x-1}{2+\cos x-\cos^2x}=\frac{\left(\sin^2x-1\right)+2\cos x}{-\left(\cos x+1\right)\left(\cos x-2\right)}\) (Đk: cosx khác -1 và 2)
\(=\frac{-\cos x\left(\cos x-2\right)}{-\left(\cos x+1\right)\left(\cos x-2\right)}\)
\(=\frac{\cos x}{1+\cos x}\)
a) Ta có: 1−sin2x1+cotx −cos2x1+tanx =1−sin2x1+cosxsinx −cos2x1+sinxcosx (Đk: sinx và cosx khác 0)
=1−sin3xsinx+cosx −cos3xcosx+sinx
=1−(sinx+cosx)(sin2x−sinx.cosx+cos2x)sinx+cosx
=1−(sin2x+cos2x−sinx.cosx) (do sinx + cosx luôn khác 0)
=sinx.cosx ( do sin2x+cos2x=1)
b) Ta có: sin2x+2cosx−12+cosx−cos2x =(sin2x−1)+2cosx−(cosx+1)(cosx−2) (Đk: cosx khác -1 và 2)
=−cosx(cosx−2)−(cosx+1)(cosx−2)
=cosx1+cosx

tam thoi cho ban dung
<=>(sinx+cosx-1)/(1-cosx+sinx+cosx-1)=(2cosx)/(sinx-cosx+1+2cosx)
<=>(sinx+cosx-1)/sinx=2cosx/(sinx+cosx+1)
x€(0;π/2)=> sinx ≠0; sinx+cosx+1≠0
<=>(sinx+cosx-1)(sinx+cosx+1)=2sinxcosx
<=>(sinx+cosx)^2-1=2sinxcosx
<=>(sin^2x+cos^2+2sinxcos)-1=2sinxcosx
<=>1+2sinxcosx-1=2sinxcosx
<=>2sinxcosx=2sinxcosx
moi bd <=>=> ban dung =>dpcm
ta có : \(0^o< x< 90^o\) \(\Rightarrow sinx-cosx+1>0\) và ta luôn có \(1-cosx>0\) \(\Rightarrow\) biểu thức trên được xác định
\(\Rightarrow\dfrac{sinx+cos-1}{1-cosx}=\dfrac{2cosx}{sinx-cos+1}\)
\(\Leftrightarrow\left(sinx+cosx-1\right)\left(sinx-cosx+1\right)=2cosx\left(1-cosx\right)\)
\(\Leftrightarrow\left(sinx+\left(cosx-1\right)\right)\left(sinx-\left(cosx-1\right)\right)=2cosx\left(1-cosx\right)\)
\(\Leftrightarrow sin^2x-\left(cosx-1\right)^2=2cosx-2cos^2x\)
\(\Leftrightarrow sin^2x-cos^2x+2cosx-1=2cosx-2cos^2x\)
\(\Leftrightarrow sin^2x-cos^2x+2cosx-sin^2x-cos^2x=2cosx-2cos^2x\)\(\Rightarrow2cosx-2cos^2x=2cosx-cos^2x\) \(\Rightarrow\left(đpcm\right)\)
iểm tra với n = 1
Giả sử đã có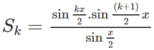
Viết S k + 1 = S k + sin ( k + 1 ) x sử dụng giả thiết quy nạp và biến đổi ta có