Cho tích phân
1. Tính I bằng cách khai triển .
2. Đặt u = 2x + 1. Biến đổi biểu thức dx thành g(u)du.
3. Tính và so sánh kết quả với I trong câu 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}u=x^2\\dv=cos2xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2xdx\\v=\dfrac{1}{2}sin2x\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{1}{2}x^2sin2x|^{\pi}_0-\int\limits^{\pi}_0x.sin2xdx\)

1)(2x+1)2+(1-2x)2=(1-2x)2+(1-2x)2=2(1-2x)2=(2-4x)2
2)x2(x-y)-(x-y)=(x2-1)(x-y)
3)(x-2)3=x3-3x22+3x22+23=x3-6x2+12x+8
mk k biết đ hay s,


Chọn D.
Xét I = ∫ 0 1 f ' x d x Đặt t = x → t 2 = x → 2 t d t = d x
Đổi cận x = 0 → t = 0 x = 1 → t = 1 . Khi đó I = 2 ∫ 0 1 t f ' ( t ) d t = 2 A
Tính A = ∫ 0 1 t f ' ( t ) d t . Đặt u = t d v = f ' t d t → d u = d t v = f t
Khi đó
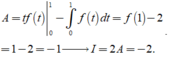
2. Vì u = 2x+1 nên du = 2dx. Ta có 2 x + 1 2 d x = u 2 d u 2