Cho hàm số f ( x ) = 1 / ( x - 2 ) có đồ thị như ở Hình 52
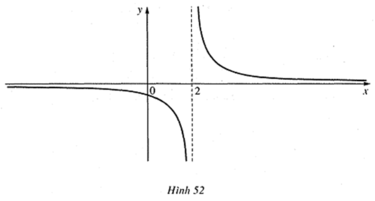
Quan sát đồ thị và cho biết:
- Khi biến x dần tới dương vô cực, thì f(x) dần tới giá trị nào.
- Khi biến x dần tới âm vô cực, thì f(x) dần tới giá trị nào.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới 0.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần tới 0.

a) Khi biến x dần tới dương vô cực thì \(f\left( x \right)\) dần tới dương vô cực.
b) Khi biến x dần tới âm vô cực thì \(f\left( x \right)\) dần âm vô cực.

a) Khi biến x dần tới 1 về bên phải thì \(f\left( x \right)\) dần dương vô cực.
b) Khi biến x dần tới 1 về bên trái thì \(f\left( x \right)\) dần âm vô cực.

a)

Giá trị \(f\left( x \right)\) trở nên rất lớn khi \(x\) dần tới 1 phía bên phải.
b)
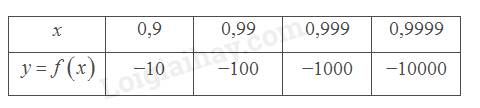
Giá trị \(f\left( x \right)\) trở nên rất bé khi \(x\) dần tới 1 phía bên trái.

a)
\(f\left( { - 2} \right) = {\left( { - 2} \right)^2} = 4;\)\(f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)
\( \Rightarrow f\left( { - 2} \right) > f\left( { - 1} \right)\)
Lấy \({x_1},{x_2} \in \left( { - 2; - 1} \right)\) sao cho \({x_1} < {x_2}\).
\( \Rightarrow {x_1} - {x_2} < 0\)
\({x_1},{x_2} < 0 \Rightarrow {x_1} + {x_2} < 0\)
Ta có:
\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) > 0\\ \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\end{array}\)
=> Hàm số nghịch biến trên (-2;-1)
Vậy hàm số giảm khi x tăng từ -2 đến -1
b)
\(\begin{array}{l}f\left( 1 \right) = 1;f\left( 2 \right) = {2^2} = 4\\ \Rightarrow f\left( 1 \right) < f\left( 2 \right)\end{array}\)
Lấy \({x_1},{x_2} \in \left( {1;2} \right)\) sao cho \({x_1} < {x_2}\).
\( \Rightarrow {x_1} - {x_2} < 0\)
\({x_1},{x_2} > 0 \Rightarrow {x_1} + {x_2} > 0\)
Ta có:
\(\begin{array}{l}f\left( {{x_1}} \right) = x_1^2;f\left( {{x_2}} \right) = x_2^2\\f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = x_1^2 - x_2^2\\ = \left( {{x_1} - {x_2}} \right).\left( {{x_1} + {x_2}} \right) < 0\\ \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\end{array}\)
=> Hàm số đồng biến trên (1;2)
Vậy hàm số tăng khi x tăng từ 1 đến 2.

Hàm số g(x) nghịch biến trên khoảng (0;1) khi ![]()
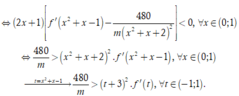
Dựa vào đồ thị, ta có
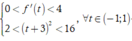
![]()
Theo YCBT 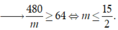
Chọn C.
- Khi biến x dần tới dương vô cực, thì f(x) dần tới giá trị 0.
- Khi biến x dần tới âm vô cực, thì f(x) dần tới giá trị 0.