Hình bên là một cái lều ở trại hè, có dạng một lăng trụ đứng kèm theo kích thước. Sau đây là ba kiểu mà học sinh lựa chọn.
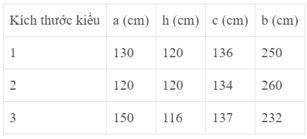
Với yêu cầu nói trên, nên chọn kiểu nào để thể tích của lều lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

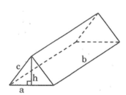
Ta có thể xem cái lều là một làng trụ đứng đáy tam giác cân cạnh bên bằng c, cạnh đáy bằng a, đường cao đáy là h, đường cao hình lăng trụ là b.
Áp dụng công thức: V = S.h, ta có:
*Kiểu 1: S=1/2 .130.120= 7800 ( c m 2 )
V = 7800.250 =1950000 ( c m 3 )
*Kiểu 2: S =1/2 .120.120 = 7200 ( c m 2 )
V = 7200.260= 1872000 ( c m 3 )
Kiểu 3: S=1/2 .150.116=8700 ( c m 2 )
V = 8700.232 = 2018400 ( c m 3 )

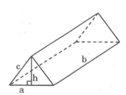
Hai mặt bên là hai hình chữ nhật bằng nhau có kích thước là c và b, có diện tích:
* Kiểu 1: Diện tích hai mặt bên là: 2(136.250)= 68000 ( c m 2 )
Phần diện tích lều được nhận ánh sáng là:
7800.2 + 68000 =83600 ( c m 2 )
*Kiểu 2: Diện tích hai mặt bên là: 2(134.280) = 69680 ( c m 2 )
Phẩn diện tích lều được nhận ánh sáng là:
7200.2 + 69680 = 84080 ( c m 2 )
*Kiểu 3: Diện tích hai mặt bên: 2(137.232) = 63568 ( c m 2 )
Phần diện tích lều đượcnhận ánh sáng là:
8700.2 + 63568=80968 ( c m 2 )

a:
-Kiểu 1: \(S=\dfrac{1}{2}\cdot130\cdot120=7800\left(cm^2\right)\)
\(V=7800\cdot250=1950000\left(cm^3\right)\)
-Kiểu 2: \(S=\dfrac{1}{2}\cdot120\cdot120=7200\left(cm^2\right)\)
\(V=7200\cdot260=1872000\left(cm^3\right)\)
-Kiểu 3: \(S=\dfrac{1}{2}\cdot150\cdot116=8700\left(cm^2\right)\)
\(V=8700\cdot232=2018400\left(cm^3\right)\)
b:
-Kiểu 1:
Diện tích hai mặt bên là:
\(2\cdot136\cdot250=68000\left(cm^2\right)\)
Phần diện tích lều nhận được ánh sáng là:
7800+68000=75800(cm2)
-Kiểu 2:
DIện tích hai mặt bên là:
\(2\cdot134\cdot260=69680\left(cm^2\right)\)
Phần diện tích lều nhận được ánh sáng là;
\(7200+69680=76880\left(cm^2\right)\)
-Kiểu 3:
Diện tích hai mặt bên là:
\(2\cdot137\cdot232=63568\left(cm^2\right)\)
Phần diện tích lều nhận được ánh sáng là:
\(63568+8700=72268\left(cm^2\right)\)
c: Chọn kiều lều 3 vì thể tích lớn nhất

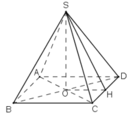
a) Lều là hình chóp đều có đáy là hình vuông cạnh bằng 2m, chiều cao bằng 2m.
Thể tích không khí trong lều bằng thể tích lều và bằng:
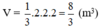
b) Số vải bạt cần thiết đề dựng lều chính là diện tích xung quanh của lều.
Dựng trung đoạn SH.
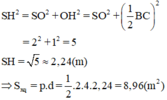

a) Lều là lăng trụ đứng tam giác.
Diện tích đáy (tam giác):
S=12.3,2.1,2=1,92(m2)S=12.3,2.1,2=1,92(m2)
Thể tích khoảng không bên trong lều là:
V = Sh = 1,92. 5 = 9,6 (m3)
b) Số vải bạt cần có để dựng lều chính là diện tích toàn phần của lăng trụ trừ đi diện tích mặt bên có kích thước là 5m và 3,2m.
Diện tích xung quanh lăng trụ là:
Sxq = 2ph = (2 + 2+ 3,2) .5 = 36 (m2)
Diện tích toàn phần:
Stp = Sxq + 2Sđ = 36 + 2.1,92 = 39,84 (m2)
Diện tích mặt bên kích thước 5m và 3,2m là:
S = 5.3,2 = 16 (m2)
Vậy số vải bạt cần có để dựng lều là:
39,84 – 16 = 23,84 (m2)
Chú ý:Có thể tính bằng cách khác là tổng diện tích hai mặt bên và hai đáy.

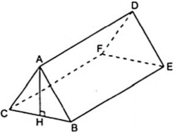
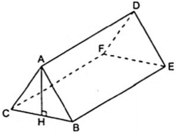
Áp dụng công thức thể tích của hình lăng trụ đứng ta có: V = S.h
Ta có:
Do đó: V = S.h = 0,6AH.2,4 = 1,44AH
Theo giả thiết ta có: 1,44AH = 2,16 ⇔ AH = 1,5( cm )

Áp dụng công thức thể tích của hình lăng trụ đứng ta có: V = S.h
Ta có: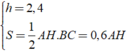
Do đó: V = S.h = 0,6AH.2,4 = 1,44AH
Theo giả thiết ta có: 1,44AH = 2,16 ⇔ AH = 1,5( cm )

a) Thể tích không khí trong chiếc lều là: \(\frac{1}{3}{.3^2}.2,8 = 8,4\) (\({m^3}\))
b) Độ dài trung đoạn của hình chóp là: \(\sqrt {2,{8^2} + 1,{5^2}} \approx 3,18\)
Diện tích vải lều là: \(\frac{{4.3}}{2}.3,18= 19,08\) (\(c{m^2}\))
Vậy chọn kiểu 3 thì thể tích lều lớn nhất.