Giải các phương trình sau: (3,5 – 7x)(0,1x + 2,3) = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. (4x−10)(24+5x)=0⇔4x−10=0(4x−10)(24+5x)=0⇔4x−10=0 hoặc 24+5x=024+5x=0
+ 4x−10=0⇔4x=10⇔x=2,54x−10=0⇔4x=10⇔x=2,5
+ 24+5x=0⇔5x=24⇔x=−4,824+5x=0⇔5x=24⇔x=−4,8
Phương trình có nghiệm x = 2,5 và x = -4,8
b. (3,5−7x)(0,1x+2,3)=0⇔3,5−7x=0(3,5−7x)(0,1x+2,3)=0⇔3,5−7x=0hoặc 0,1x+2,3=00,1x+2,3=0
+ 3,5−7x=0⇔3,5=7x⇔x=0,53,5−7x=0⇔3,5=7x⇔x=0,5
+ 0,1x+2,3=0⇔0,1x=−2,3⇔x=−230,1x+2,3=0⇔0,1x=−2,3⇔x=−23
Phương trình có nghiệm x =0,5 hoặc x = -23

e) \(⇔\left[\begin{array}{} x-1=0\\\ 2x+7=0\\ x^2+2=0 \end{array}\right.\)\(⇔\left[\begin{array}{} x=1\\\ x=-\frac{7}{2}\\ x^2=-2(ko.xảy.ra) \end{array}\right.\)\(⇔\left[\begin{array}{} x=1\\ x=-\frac{7}{2} \end{array}\right.\)
\(f) ⇔\left[\begin{array}{} 4x-10=0\\ 24+5x=0 \end{array}\right.\)\(⇔\left[\begin{array}{} x=\frac{10}{4}\\ x=-\frac{24}{5} \end{array}\right.\)
\(g) ⇔\left[\begin{array}{} 3,5-7x=0\\ 0,1x+2,3=0 \end{array}\right.⇔\left[\begin{array}{} x=0,5\\ x=-23 \end{array}\right.\)
\(h) ⇔\left[\begin{array}{} 5x+2=0\\ x-7=0 \end{array}\right.⇔\left[\begin{array}{} x=-\frac{2}{5}\\ x=7 \end{array}\right.\)

a) \(\left(4x-10\right)\left(24+5x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}4x-10=0\\24+5x=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{10}{4}=\dfrac{5}{2}\\x=-\dfrac{24}{5}\end{matrix}\right.\)
Vậy \(S=\left\{-\dfrac{24}{5};\dfrac{5}{2}\right\}\)
b) \(\left(3.5-7x\right)\left(0.1x+2.3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3.5-7x=0\\0.1x+2.3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3.5}{7}=\dfrac{1}{2}\\x=-\dfrac{2.3}{0.1}=-23\end{matrix}\right.\)
Vậy \(S=\left\{-23;\dfrac{1}{2}\right\}\)

a: (3x-2)(4x+5)=0
=>3x-2=0 hoặc 4x+5=0
=>x=2/3 hoặc x=-5/4
b: (2,3x-6,9)(0,1x+2)=0
=>2,3x-6,9=0 hoặc 0,1x+2=0
=>x=3 hoặc x=-20
c: =>(x-3)(2x+5)=0
=>x-3=0 hoặc 2x+5=0
=>x=3 hoặc x=-5/2

a) (3x - 2)(4x + 5) = 0
\(\Leftrightarrow\orbr{\begin{cases}3x-2=0\\4x+5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{2}{3}\\x=-\frac{5}{4}\end{cases}}}\)
Vậy \(S=\left\{-\frac{5}{4};\frac{2}{3}\right\}\)
b) (2,3x - 6,9)(0,1x + 2) = 0
\(\Leftrightarrow\orbr{\begin{cases}2,3x-6,9=0\\0,1x+2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=-20\end{cases}}}\)
Vậy \(S=\left\{-20;3\right\}\)

\(A.\left(2,3x-6,5\right)\left(0,1x+2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}2,3x-6,5=0\\0,1x+2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}2,3x=6,5\\0,1x=-2\end{cases}}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{6,5}{2,3}\\x=-20\end{cases}}\)

3(2,2 – 0,3x) = 2,6 + (0,1x – 4)
⇔ 6,6 – 0,9x = 2,6 + 0,1x – 4 ⇔ 6,6 – 2,6 + 4 = 0,1x + 0,9x
⇔ x = 8
Phương trình có nghiệm x = 8

a, (3x-2)(4x+5)=0
↔ TH1: 3x-2 = 0 ↔ x = 2/3
TH2 : 4x+5 = 0 ↔ x = -5/4
Vậy PT có tập no S = ( 2/3; -5/4)
b,(2,3x-6,9)(0,1x+2)=0
↔ TH1: 2,3x - 6,9 = 0 ↔ x = 3
TH2 : 0,1x + 2 = 0 ↔ x = -20
Vậy PT có tập no S = ( 3; -20)
c, (4x+2)(x^2 +1)=0
TH1: 4x+2=0 ↔ x = -1/2
Th2 : x^2 +1≠0 ( vô lí)
Vậy PT có tập no S = (-1/2)
d, (2x+7)(x-5)(5x+1)=0
↔ TH1: 2x+7 = 0 ↔ x = -7/2
TH2: x-5 = 0 ↔ x = 5
TH3 : 5x+1 = 0 ↔ x = -1/5
Vậy PT có tập no S = ( -7/2 ; 5 ; -1/5
a, \(\left(3x-2\right)\left(4x+5\right)=0\Leftrightarrow x=\frac{2}{3};x=-\frac{5}{4}\)
b, \(\left(2,3-6,9\right)\left(0,1x+2\right)=0\Leftrightarrow\frac{x}{10}+2=0\Rightarrow x=-20\)
c, \(\left(4x+2\right)\left(x^2+1>0\right)=0\Leftrightarrow x=-\frac{1}{2}\)

(2,3x – 6,9).(0,1x + 2) = 0
⇔ 2,3x – 6,9 = 0 hoặc 0,1x + 2 = 0
+ 2,3x – 6,9 = 0 ⇔ 2,3x = 6,9 ⇔ x = 3.
+ 0,1x + 2 = 0 ⇔ 0,1x = -2 ⇔ x = -20.
Vậy phương trình có tập nghiệm S = {3; -20}.
c) (4x + 2)(x2 + 1) = 0
⇔ 4x + 2 = 0 hoặc x2 + 1 = 0
+ 4x + 2 = 0 ⇔ 4x = -2 ⇔ x = 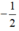
+ x2 + 1 = 0 ⇔ x2 = -1 (Phương trình vô nghiệm vì x2 ≥ 0 với mọi x ).
Vậy phương trình có tập nghiệm 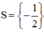
(3,5 – 7x)(0,1x + 2,3) = 0 ⇔ 3,5 – 7x = 0 hoặc 0,1x + 2,3 = 0
3,5 – 7x = 0 ⇔ 3,5 = 7x ⇔ x = 0,5
0,1x + 2,3 = 0 ⇔ 0,1x = - 2,3 ⇔ x = -23
Phương trình có nghiệm x = 0,5 hoặc x = -23