Cho hình thoi ABCD có góc ∠A = 60o. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


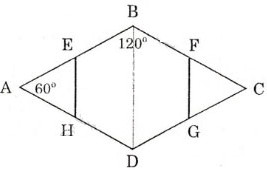
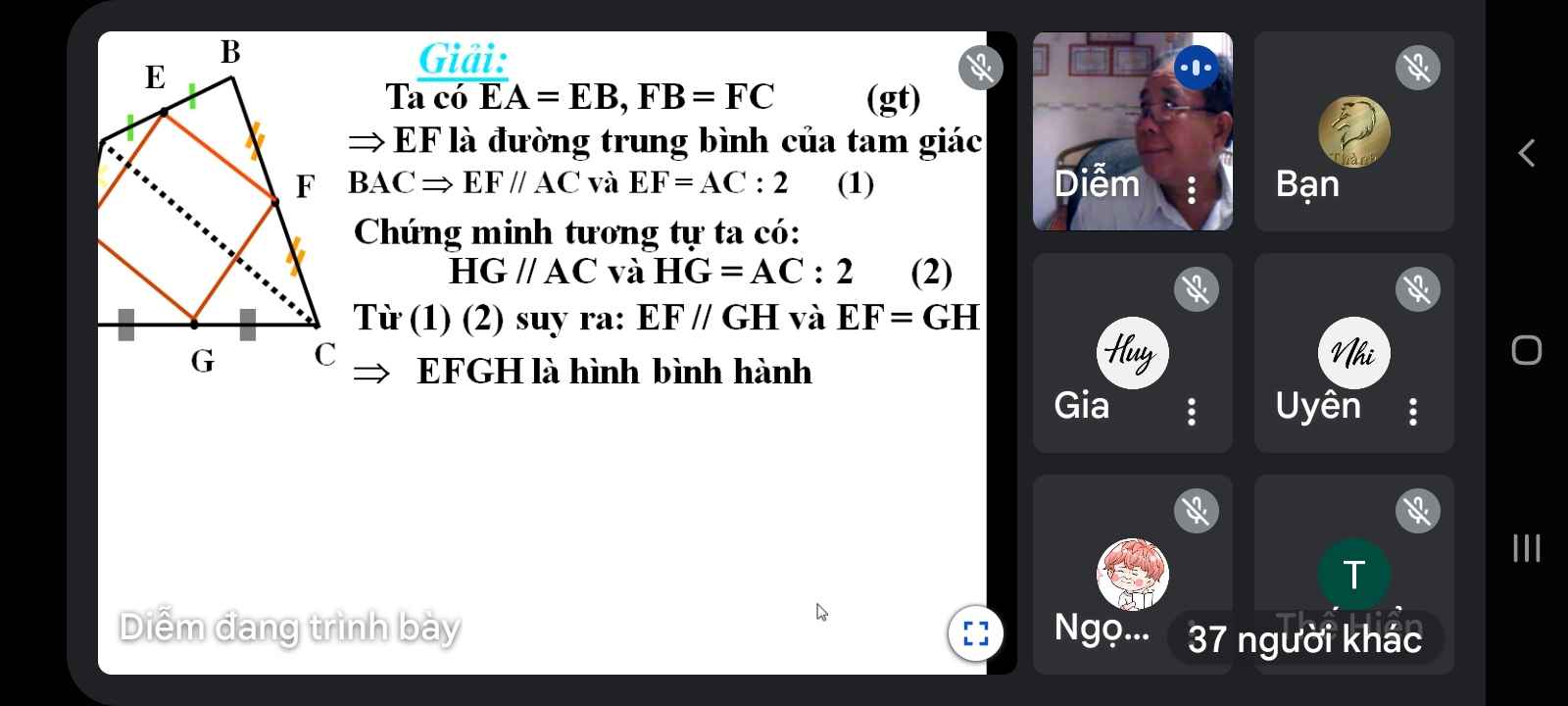
ABCD là hình thoi,  =
=  nên
nên 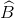 =
=  ,
,  =
=  .
.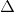 EAH là tam giác đều (vì tam giác cân có một góc
EAH là tam giác đều (vì tam giác cân có một góc  ) nên
) nên 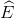 =
=  ,
,  =
=  . Cũng thế
. Cũng thế  =
=  ,
,  =
=  .
.
Vậy EBFGDH có tất cả các góc bằng nhau, mặt khác EBFGDH cũng có tất cả các cạnh bằng nhau( bằng nửa cạnh hình thoi)
Vậy EBFGDH là một lục giác đều

ABCD là hình thoi,  =
=  nên
nên  =
=  ,
,  =
=  .
. EAH là tam giác đều (vì tam giác cân có một góc
EAH là tam giác đều (vì tam giác cân có một góc  ) nên
) nên  =
=  ,
,  =
=  . Cũng thế
. Cũng thế  =
=  ,
,  =
=  .
.
Vậy EBFGDH có tất cả các góc bằng nhau, mặt khác EBFGDH cũng có tất cả các cạnh bằng nhau( bằng nửa cạnh hình thoi)
Vậy EBFGDH là một lục giác đều

Bạn tham khảo ở link này nha :
https://h.vn/hoi-dap/question/246529.html
~~ Hok tốt ~~

Chứng minh được M Q = N P = 1 2 B D
Chứng minh tam giác ABD đều, suy ra được MN = BN = NP PD = DQ = QM
Chứng minh các góc của đa giác MBNPDQ bằng nhau và cùng bằng 1200.
Từ đó quy ra đa giác MBNPDQ là lục giác đều (ĐPCM).

Số đo một góc trong lục giác đều là :\(180\times\left(6-2\right):6=720:6=120\left(độ\right)\)
ABCD là hình thoi =>AB=BC=CD=AD hay 1/2AB=1/2BC=1/2CD=1/2AD
Tam giác AHE có AH=AE (AH=1/2AD;AE=1/2AB)
=> Tam giác AHE cân . Mà A =60 (độ)
=> Tam giác AHE đều nên AHE=AEH=60 (độ)
Mặt khác góc DHE và góc HEB lần lượt kề bù vs AHE và AEH
=>DHE=HEB=120 (độ)
C/m tương tự ta có : HGF=BFG=120 (độ)
Lại có : ABCD là hình thoi có A =60 =>C=60 và D=B=120 (độ)
Lục giác HEBFGD có số đo mỗi góc bằng 120(độ) (cmt)
=> HEBFGD là lục giác đều
....................Đpcm
Hay cách khác cậu có thể c/m lục giác đều bằng cách c/m 6 cạnh bằng nhau thì sẽ dễ và nhanh hơn cách làm này,đương nhiên mk cux pit c/m cách lm đó n mk k tkick z pn tham khảo cách làm này na mặc dù nó hơi dài .!!!

Xét ΔABD có AB=AD và góc BAD=60 độ
nên ΔABD đều
Ta có: ΔDAB cân tại D
mà DE là đường trung tuyến
nên DE vuông góc với BE
=>E nằm trên đường tròn đường kính BD(1)
Ta có:ΔBAD cân tại B
ma BH là đường trung tuyến
nên BH vuông góc với HD
=>H nằm trên đường tròn đường kính BD(2)
Xét ΔCBD có CB=CD và góc BCD=60 độ
nên ΔCBD đều
Ta có: ΔBDC cân tại D
mà DF là đường trung tuyến
nen DF vuông góc với BF
=>F nằm trên đường tròn đường kính BD(3)
Ta có: ΔBDC cân tại B
mà BG là đường trung tuyến
nên BG vuông góc với GD
=>G nằm trên đường tròn đường kính BD(4)
Từ (1), (2), (3) và (4) suy ra E,B,F,G,D,H cùng nằm trên 1 đường tròn

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

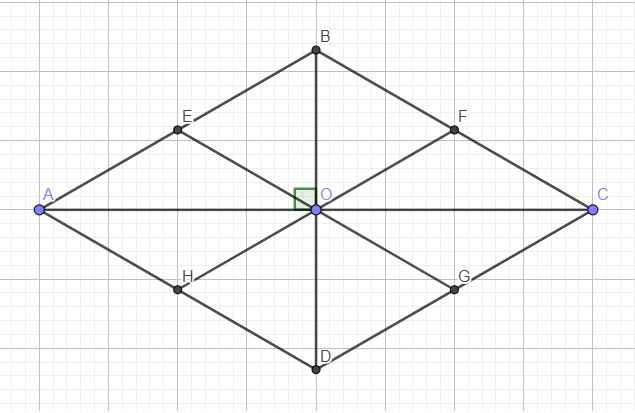
Do ABCD là hình thoi \(\Rightarrow\Delta BCD\) cân tại C
Mà \(C=60^0\Rightarrow\Delta BCD\) đều
Hoàn toàn tương tự, ta có tam giác ABD đều
\(\Rightarrow AB=BC=CD=DA=BD\) (1)
Gọi O là giao điểm 2 đường chéo \(\Rightarrow OA\perp OB\)
Trong tam giác vuông OAB, do E là trung điểm AB nên OE là trung tuyến ứng với cạnh huyền
\(\Rightarrow OE=\dfrac{1}{2}AB\) (2)
Mà O là trung điểm BD (tính chất hình thoi) \(\Rightarrow OB=\dfrac{1}{2}BD\) (3)
(1);(2);(3) \(\Rightarrow OE=OB\)
Hoàn toàn tương tự, ta có:
\(OE=OB=OF=OG=OD=OH\)
\(\Rightarrow\) Các điểm E, B, F, G, D, H cùng thuộc 1 đường tròn tâm O bán kính OB

Áp dụng tính chất đường trung bình của tam giác ta chứng minh được:
E H = F G = 1 2 B D v à H G = E F = 1 2 A C
Mà AC = BD Þ EH = HG = GF= FE nên EFGH là hình thoi.
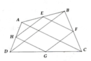

+ ABCD là hình thoi
⇒ AD // BC
+ ABCD là hình thoi ⇒ AB = BC = CD = DA
Mà E, F, G, H là trung điểm của 4 đoạn thẳng trên
⇒ AE = EB = BF = FC = CG = GD = DH = HA.
ΔAEH có góc A = 60º và AE = AH nên là tam giác đều
+ Lại có ΔAEH đều
⇒ EH = AH = AE.
Chứng minh tương tự : FG = FC = CG
⇒ EB = BF = FG = GD = DH = HE.
Vậy EBFGDH có tất cả các góc bằng nhau và tất cả các cạnh bằng nhau nên là lục giác đều.