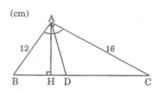
Tam giác ABC có góc A = 90 0 , AB = 12cm, AC=16cm; đường phân giác góc A cắt BC tại D. Tính BC, BD và DC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác \(ABC\)vuông tại \(A\):
\(BC^2=AB^2+AC^2\)(định lí Pythagore)
\(=12^2+16^2=400\)
\(\Leftrightarrow BC=20\left(cm\right)\)
\(AB^2=BD.BC\Leftrightarrow BD=\frac{AB^2}{BC}=\frac{12^2}{20}=7,2\left(cm\right)\)
Xét tam giác \(ABC\)phân giác \(AD\):
\(\frac{AB}{BD}=\frac{AC}{CD}\)(tính chất đường phân giác)
\(=\frac{AB+AC}{BD+CD}=\frac{12+16}{20}=1,4\)
\(\Leftrightarrow BD=\frac{AB}{1,4}=\frac{12}{1,4}=\frac{60}{7}\left(cm\right)\)
\(HD=\left|BD-BH\right|=\frac{48}{35}\left(cm\right)\)

a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2 = AB2 + AC2 = 122 + 162 = 400
Suy ra: BC =20 (cm)
Vì AD là đường phân giác của ∠(BAC) nên:
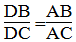
Suy ra:
Suy ra:
Vậy : DC = BC – DB = 20 - 60/7 = 80/7 (cm)
b. Ta có: SABC =1/2.AB.AC =1/2.AH.BC
Suy ra: AB.AC = AH.BC
Trong tam giác vuông AHB, ta có: ∠(AHB ) = 90o
Theo định lí Pi-ta-go, ta có: AB2 = AH2 + HB2
Suy ra: HB2 = AB2 - AH2 = 122 - (9,6)2 = 51,84 ⇒ HB =7,2 (cm)
Vậy HD = BD – HB = 607 - 7,2 ≈ 1,37 (cm)
Trong tam giác vuông AHD, ta có: ∠(AHD) = 90o
Theo định lí Pi-ta-go, ta có:
AD2 = AH2 + HD2 = (9,6)2 + (1,37)2 = 94,0369
Suy ra: AD ≈ 9,70 (cm)

A B C 16 12 H
1) Có \(\Delta ABC\) vuông
=> S\(\Delta ABC\) = \(\dfrac{AB.AC}{2}\) = \(\dfrac{16.12}{2}\) = 96 (cm2)
2) Có \(\Delta ABC\) vuông , theo định lý Pytago ta có :
AB2 + AC2 = BC2
=> 162 + 122 = BC2
=> 400 = BC2
=> BC = 20 (cm)
Ta có : S\(\Delta ABC\) = S\(\Delta ABH\) + S\(\Delta ACH\)
=> \(\dfrac{BH.AH}{2}+\dfrac{HC.AH}{2}=S\Delta ABC\)
=> \(\dfrac{BH.AH+HC.AH}{2}=S\Delta ABC\)
=> \(\dfrac{AH.\left(BH+HC\right)}{2}=S\Delta ABC\)
=> \(\dfrac{AH.BC}{2}\) = 96
=> AH = 96 . \(\dfrac{2}{BC}\) = 96 . \(\dfrac{2}{20}\) = 9.6 (cm)
3) Có \(\Delta ABH\) vuông , theo định lý Pytago ta có :
BH2 = AB2 - AH2
=>BH2 = 162 - 9.62 = 163.84
=> BH = 12.8 (cm)
=> CH = BC - BH = 20 - 12.8 = 7.2 (cm)

Ta có: S A B C = 1/2.AB.AC = 1/2.AH.BC
Suy ra: AB.AC = AH.BC
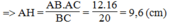
Trong tam giác vuông AHB, ta có: ∠ A H B = 90 0
Theo định lí Pi-ta-go, ta có: A B 2 = A H 2 + H B 2
Suy ra: H B 2 = A B 2 - A H 2 = 12 2 - 9 , 6 2 = 51,84 ⇒ HB =7,2 (cm)
Vậy HD = BD – HB = 60/7 - 7,2 ≈ 1,37 (cm)
Trong tam giác vuông AHD, ta có: ∠ A H D = 90 0
Theo định lí Pi-ta-go, ta có:
A D 2 = A H 2 + H D 2 = 9 , 6 2 + 1 , 37 2 = 94,0369
Suy ra: AD ≈ 9,70 (cm)

3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)

ΔCID vuông tại I
=>\(CI^2+ID^2=CD^2\)
=>\(DI=\sqrt{6^2-3.6^2}=4.8\left(cm\right)\)
Kẻ AH vuông góc BC
=>AH//DI
Xét ΔCAH có DI//AH
nên \(\dfrac{DI}{AH}=\dfrac{CD}{CA}=\dfrac{1}{2}\)
=>\(AH=9.6\left(cm\right)\)
ΔAHB vuông tại H
=>\(AB^2=AH^2+HB^2\)
=>\(HB=\sqrt{16^2-9.6^2}=12.8\left(cm\right)\)
ΔAHC vuông tại H
=>\(AH^2+HC^2=AC^2\)
=>\(HC=\sqrt{12^2-9.6^2}=7.2\left(cm\right)\)
BC=BH+CH
=12,8+7,2
=20(cm)
Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = 12 2 + 6 2 = 400
Suy ra: BC =20 (cm)
Vì AD là đường phân giác của ∠(BAC) nên:
Suy ra: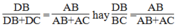
Suy ra: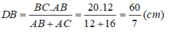
Vậy : DC = BC – DB = 20 - 60/7 = 80/7 (cm)