Trong Δ ABC có AB = 8cm và B'C'//BC. Lấy trên cạnh AB điểm B', trên cạnh AC lấy điểm C' sao cho AB' = 2cm, AC' = 3cm. Tính độ dài cạnh AC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo định lý Ta - let ta có:
\(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\)
\(\Leftrightarrow\dfrac{4}{6}=\dfrac{3}{AC}\)
\(\Rightarrow\dfrac{2}{3}=\dfrac{1}{AC}\)
\(\Rightarrow2AC=3\)
\(\Rightarrow AC=\dfrac{2}{3}\)

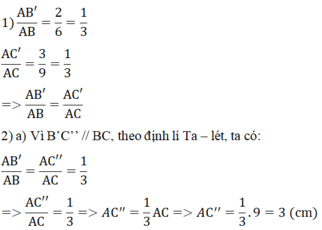
b) Trên đoạn thẳng AC ta có: AC’= AC’’= 3 cm nên
Khi đó, hai đường thẳng BC và B’C’ song song với nhau.

a, Ta có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{6}{8}=\dfrac{7,5}{10}=\dfrac{3}{4}\)
=> MN // BC (Ta lét đảo)
b, Vì MN // BC
Theo hệ quả Ta lét \(\dfrac{AM}{AB}=\dfrac{MN}{BC}\Leftrightarrow\dfrac{6}{8}=\dfrac{MN}{12}\Leftrightarrow MN=9cm\)

Sửa đề: ΔABC vuông tại A
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
vậy: BC=10cm
b) Xét ΔAMC và ΔEMB có
CM=BM(M là trung điểm của BC)
\(\widehat{AMC}=\widehat{BME}\)(hai góc đối đỉnh)
MA=ME(gt)
Do đó: ΔAMC=ΔEMB(c-g-c)
Suy ra: AC=BE(hai cạnh tương ứng)
Xét ΔAMB và ΔEMC có
AM=EM(gt)
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔAMB=ΔEMC(c-g-c)
Suy ra: \(\widehat{BAM}=\widehat{CEM}\)(hai góc tương ứng)
mà \(\widehat{BAM}\) và \(\widehat{CEM}\) là hai góc ở vị trí so le trong
nên AB//EC(Dấu hiệu nhận biết hai đường thẳng song song)

a) Ta có:
\(\frac{{AE}}{{AC}} = \frac{{10}}{{15}} = \frac{2}{3};\frac{{AF}}{{AB}} = \frac{8}{{12}} = \frac{2}{3}\)
Xét tam giác \(AFE\) và tam giác \(ABC\) ta có:
\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}} = \frac{2}{3}\)
\(\widehat A\) chung
Do đó, \(\Delta AFE\backsim\Delta ABC\) (c.g.c)
Do đó, \(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}} = \frac{{EF}}{{BC}} = \frac{2}{3}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Do đó, \(\frac{{EF}}{{BC}} = \frac{2}{3} \Rightarrow EF = \frac{{BC.2}}{3} = \frac{{18.2}}{3} = 12\)
Vậy \(BC = 12cm\).
b) Vì \(FC = FD\) nên tam giác \(FDC\) cân tại \(F\).
Suy ra, \(\widehat {FDC} = \widehat {FCD}\) (tính chất)
Ta có:
\(\frac{{AC}}{{MD}} = \frac{{15}}{{20}} = \frac{3}{4};\frac{{BC}}{{DE}} = \frac{9}{{12}} = \frac{3}{4}\)
Xét tam giác \(ABC\) và tam giác \(MED\) ta có:
\(\frac{{AC}}{{MD}} = \frac{{BC}}{{DE}} = \frac{3}{4}\)
\(\widehat {FCD} = \widehat {FDC}\) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta MED\) (c.g.c).
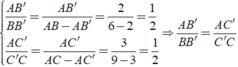
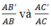
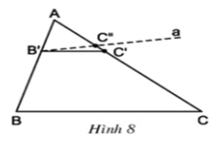

Áp dụng hệ quả trên ta có: Δ ABC, B'C'//BC; B' ∈ AB, C' ∈ AC
Khi đó ta có: AB'/AB = AC'/AC ⇔ 2/8 = 3/AC ⇒ AC = (3.8)/2 = 12( cm )