Cho hình chữ nhật ABCD. Điểm E thuộc cạnh AD, điểm F thuộc cạnh AB. Gọi I, K, M, N theo thứ tự là trung điểm của EF, FD, BE, BD. Chứng minh IN = KM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


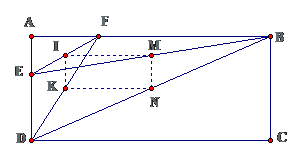
Ta đi chứng minh tứ giác IKMN là hình chữ nhật
+) Theo giả thiết có : là hình bình hành
+) là hình chữ nhật

Xét tam giác FEB ta có
\(\hept{\begin{cases}EI=IF\left(gt\right)\\EM=MB\left(gt\right)\end{cases}}\)
=> IM là đường trung bình của tam giác FEB
IM=1/2FB
\(\hept{\begin{cases}IMsongsongFB\\màAnằmtrenFB\end{cases}}\)
=> IM // AB(1)
Xét tam giác FDB có
\(\hept{\begin{cases}DK=KF\left(gt\right)\\DN=NB\left(gt\right)\end{cases}}\)
=>KN là đường trung bình cảu tam giác FDB
=> KN = 1/2 DB
\(\hept{\begin{cases}IM=\frac{1}{2}FB\left(cmt\right)\\KN=\frac{1}{2FB}\left(cmt\right)\end{cases}}\)
=>IM=KN(2)
Từ (1) và (2) => IMKN là hình bình hành
Xét tam giác EFD có
\(\hept{\begin{cases}EI=IF\left(gt\right)\\DK=KF\left(gt\right)\end{cases}}\)
=> IK là đường trung bình của tam giác EFD
\(\hept{\begin{cases}=>IKsongsongED\\màĂtrenED\end{cases}}\)
\(\hept{\begin{cases}=>IKsongsongDA\\ADvuonggocAB\left(hìnhchunhatABCD\right)\end{cases}}\)
\(\hept{\begin{cases}=>IKvuonggocAB\\IMsongsongAB\left(cmt\right)\end{cases}}\)
=>IM vuông góc IK
=> IKMN là hình chữ nhật
=>IN=KM
HS chứng minh IMNK là hình chữ nhật Þ IN = KM