Tìm tập hợp nghiệm của phương trình + = 32
A. {100} B. {10}
C. {100;10} D. {4}
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Ta có: f(x + 1) = log2(x + 1) và g(x + 2) = log2(2 - x)
![]()
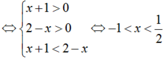

Ta có:
\({x^2} - 2x - 3 = 0 \Leftrightarrow (x + 1)(x - 3) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 3\end{array} \right. \Rightarrow E = \{ - 1;3\} \)
Lại có: \((x + 1)(2x - 3) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = \frac{3}{2}\end{array} \right.\)
\( \Rightarrow G = \left\{ { - 1;\frac{3}{2}} \right\}\)
\( \Rightarrow P = E \cap G = \left\{ { - 1} \right\}\).
Xét phương trình \(x^2-2x-3=0\) có: \(a-b+c=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{c}{a}=3\end{matrix}\right.\Rightarrow E=\left\{-1;3\right\}.\)
Xét phương trình \(\left(x+1\right)\left(2x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+1=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{2}\end{matrix}\right.\Rightarrow G=\left\{-1;\dfrac{3}{2}\right\}.\)
\(\Rightarrow P=E\cap G=\left\{-1\right\}.\)

\(\sqrt{2-f\left(x\right)}=f\left(x\right)\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)\ge0\\f^2\left(x\right)+f\left(x\right)-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\f\left(x\right)=-2< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow f\left(1\right)=f\left(2\right)=f\left(3\right)=1\)
\(\sqrt{2g\left(x\right)-1}+\sqrt[3]{3g\left(x\right)-2}=2.g\left(x\right)\)
\(VT=1.\sqrt{2g\left(x\right)-1}+1.1\sqrt[3]{3g\left(x\right)-2}\)
\(VT\le\dfrac{1}{2}\left(1+2g\left(x\right)-1\right)+\dfrac{1}{3}\left(1+1+3g\left(x\right)-2\right)\)
\(\Leftrightarrow VT\le2g\left(x\right)\)
Dấu "=" xảy ra khi và chỉ khi \(g\left(x\right)=1\)
\(\Rightarrow g\left(0\right)=g\left(3\right)=g\left(4\right)=g\left(5\right)=1\)
Để các căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}f\left(x\right)-1\ge0\\g\left(x\right)-1\ge0\end{matrix}\right.\)
Ta có:
\(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)-f\left(x\right)-g\left(x\right)+1=0\)
\(\Leftrightarrow\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+\left[f\left(x\right)-1\right]\left[g\left(x\right)-1\right]=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\g\left(x\right)=1\end{matrix}\right.\) \(\Leftrightarrow x=3\)
Vậy tập nghiệm của pt đã cho có đúng 1 phần tử

a. f(x) = g(x) - h(x)
\(=\left(4x^2+3x+1\right)-\left(3x^2-2x-3\right)\)
\(=4x^2+3x+1-3x^2+2x+3\)
\(=x^2+5x+4\)
Vậy \(f\left(x\right)=x^2+5x+4\)
b. Ta có: \(f\left(-4\right)=\left(-4\right)^2+5\cdot\left(-4\right)+4\)
\(=16-20+4\)
\(=-4+4=0\)
\(\Rightarrow\) -4 là nghiệm của đa thức f(x)
c. \(f\left(x\right)=0\Rightarrow x^2+5x+4=0\)
\(\Rightarrow x=\dfrac{-5\pm\sqrt{5^2-4\cdot1\cdot4}}{2\cdot1}\)
\(\Rightarrow x=\dfrac{-5\pm\sqrt{25-16}}{2}\)
\(\Rightarrow x=\dfrac{-5\pm\sqrt{9}}{2}=\dfrac{-5\pm3}{2}\)
\(\Rightarrow x=\left[{}\begin{matrix}\dfrac{-5+3}{2}=-\dfrac{2}{2}=-1\\\dfrac{-5-3}{2}=-\dfrac{8}{2}=-4\end{matrix}\right.\)
Vậy nghiệm của f(x) là -1 hoặc -4
Cho 2 số hữu tỉ a phần m và b phần m (a,b,m thuộc Z , m > 0 )
Chứng minh rằng a phần m < b phần m , thì a phần m < a+b phần m < b phần m
Trả lời câu hỏi giùm mình nha !
Đáp án : A.
Hướng dẫn: Thử kết quả trực tiếp bằng máy tính.