Cho tam giác ABC có góc A = 60o, BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Ta nhớ lại công thức, trong tam giác $ABC$ có $AB=c, BC=a, CA=b$ thì:
$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$.
Ứng vào bài toán, với $\sin A=\sin 120=\frac{\sqrt{3}}{2}$ và $a=BC=6$ thì:
$R=\frac{a}{2\sin A}=\frac{6}{2.\frac{\sqrt{3}}{2}}=2\sqrt{3}$

Chọn B.
Áp dụng định lí Cosin, ta có
BC2 = AB2 + AC2 - 2AB.AC.cosA
= 32 + 62-2.3.6.cos600 = 27
Ta thấy: BC2 + AB2 = AC2
Suy ra tam giác ABC vuông tại B
do đó bán kính R = AC : 2 = 3.

\(\cos ABC=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
\(\Leftrightarrow89a^2-AC^2=2\cdot5a\cdot8a\cdot\dfrac{1}{2}=40a^2\)
=>AC=7a
\(AM=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{25a^2+49a^2}{2}-\dfrac{64a^2}{4}=37a^2-16a^2=21a^2\)
hay \(AM=a\sqrt{21}\left(cm\right)\)
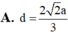
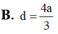
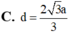
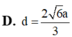
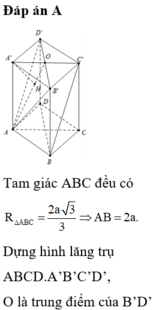
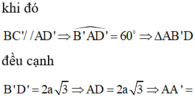
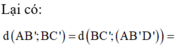
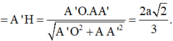
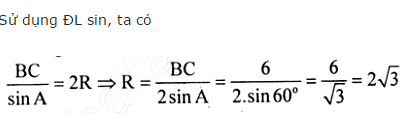
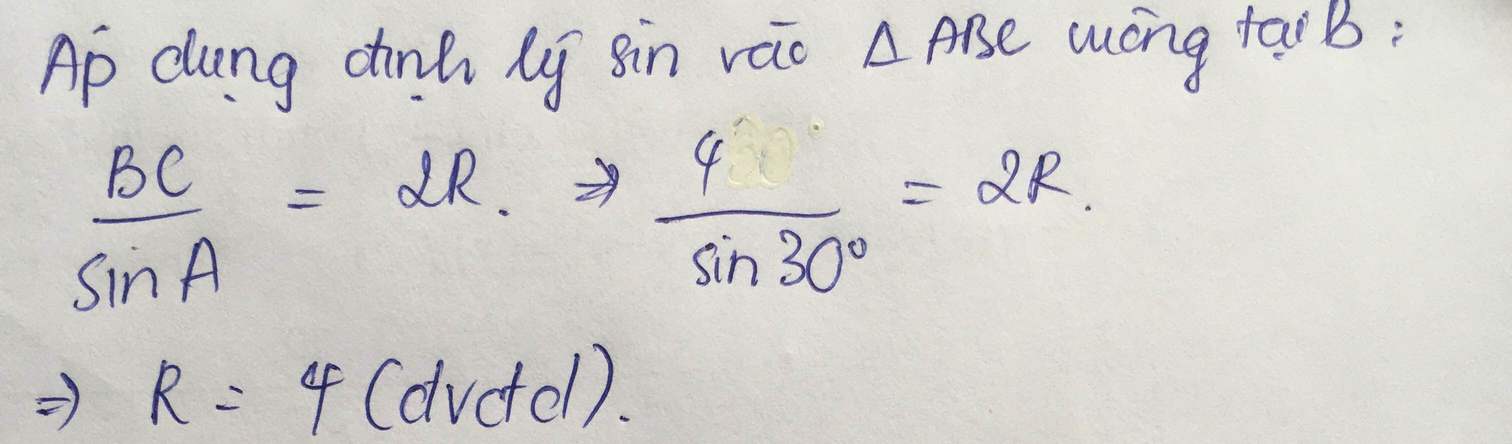
Áp dụng định lý Sin trong tam giác ABC ta có:
Vậy bán kính đường tròn ngoại tiếp tam giác bằng 2√3.