Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = - 70 o với A(1; 0). Gọi M 1 là điểm đối xứng của M qua đường phân giác của góc phần tư thứ I. Số đo của cung lượng giác A M 1 là
A . - 150 ο B . 220 ο C . 160 ο D . - 160 ο
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

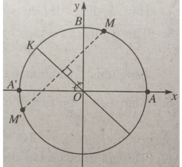
Sđ MK = sđ KM’ = 55 o
⇒ sđ AM’ = sđ AM + sđ MK + sđ KM’ = 190 o .
Đáp án: C

-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.
Vậy (-5π)/2 < -6,32 < -2π.
Do đó điểm M nằm ở góc phần tư thứ II.
Đáp án: B

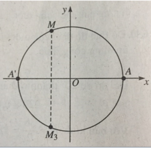
(h.66) Ta có
A M 2 = MA’ = MA + AA’
Suy ra
Sđ A M 2 = -α + π + k2π, k ∈ Z.
Vậy đáp án là B.
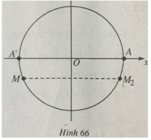
6.13. (h.67) Ta có
Sđ A M 3 = -sđ AM = -α + k2π, k ∈ Z.
Đáp án: D

a) Nếu k = 2n +1 (n ∈ Z) (thì kπ = (2n + 1)π = 2nπ + π nên M ≡ M1
Nếu k = 2n (n ∈ Z) thì kπ = 2nπ nên M ≡ A

b)
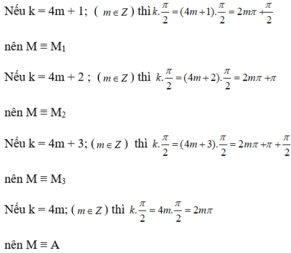
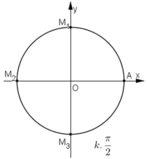
c)
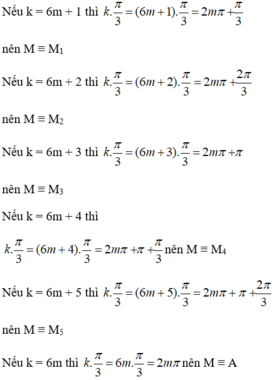
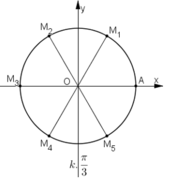

Tham khảo:
a) 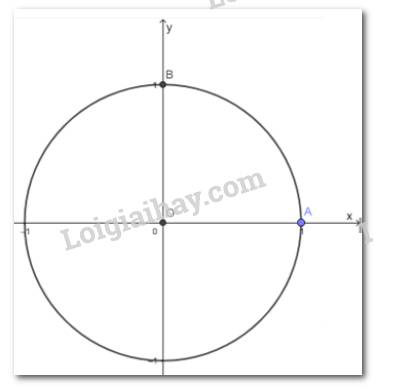
Góc lượng giác \(\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}\)
b)

Tham khảo:
a) Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó điểm M là điểm biểu diễn bởi góc có số đo \(\frac{{5\pi }}{6}\)
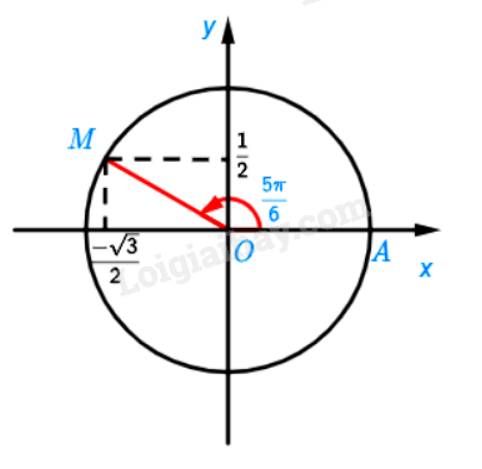
b) Ta có:
\(\sin \left( {\frac{{5\pi }}{6}} \right) = \frac{1}{2};\cos \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{2};\tan \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{3};\cot \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - 3}}{{\sqrt 3 }}\)
Cách 1. Suy luận.
Điểm M nằm ở góc phần tư thứ IV nên điểm M 1 nằm ở góc phần tư thứ hai. Số đo A M 1 dương nên hai phương án A, D bị loại. Mặt khác sđ A M 1 < 180 o nên phương án B bị loại.
Vậy đáp án là C.
Cách 2. Tính trực tiếp.
Gọi B là giao điểm của đường phân giác góc xOy với đường tròn. Ta có
Sđ A B = 45 o , s đ M A = 70 o
Suy ra sđ MB = 115 o .
Mà sđ B M 1 = sđ MB nên sđ A M 1 = 45 o + 115 o = 160 o .
Đáp án: C