Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Trả lời câu hỏi của tôi đi. Tí tôi trả lời của bạn chings xác 100% luôn. UY TÍN BẠN NHÉ
a) \(M\left(x\right)=-x^6+x^4-4x^3+x^2-5\)
\(N\left(x\right)=2x^5-x^4-x^3+x^2+x-1\)
b)\(M\left(x\right)+N\left(x\right)=-x^6+x^4-4x^3+x^2-5+2x^5-x^4-x^3+x^2+x-1\) \(=-x^6+2x^5-5x^3+2x^2+x-6\)
Vậy...
\(M\left(x\right)-N\left(x\right)=-x^6+x^4-4x^3+x^2-5-\left(2x^5+x^4-x^3+x^2-x-1\right)\)\(=-x^6+x^4-4x^3+x^2-5-2x^5+x^4+x^3-x^2+x+1\) \(=-x^6-2x^5+2x^4-3x^3+x-4\) Vậy...
c) -N(x)+M(x)=.........
a. M(x) = 3x2- 5+ x4- 3x3- x6- 2x2- x3
= - 5+ (3x2- 2x2)+(-3x3- x3)+ x4- x6
= - 5 +x2+ (-4x3) +x4 -x6
N(x) = x3 + 2x5 -x4 +x2 -2x3 +x-1
= -1+x+x2+(x3- 2x3) -x4+ 2x5
= -1+ x+ x2+ (-x3) -x4+ 2x5
b. M(x) +N(x)= (- 5 +x2 -4x3 +x4 -x6) + (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1+ x+ x2 -x3 -x4+ 2x5
= (-5-1) + x +( x2 +x2) +(-4x3-x3) +(x4-x4) +2x5 -x6
= -6 +x +2x2 +(-5x3) +0 +2x5-x6
= -6 +x +2x2 +(-5x3) +2x5-x6
M(x) -N(x)= (- 5 +x2 -4x3 +x4 -x6) - (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1-x -x2 +x3 +x4 -2x5
= (-5-1) +x +(x2-x2) +(-4x3+x3) +(x4+x4) -2x5 -x6
= -6 +x +0 +(-3x3) +2x4 -2x5 -x6
= -6 +x +(-3x3) +2x4 -2x5 -x6
a. M(x) = 3x2- 5+ x4- 3x3- x6- 2x2- x3
= - 5+ (3x2- 2x2)+(-3x3- x3)+ x4- x6
= - 5 +x2+ (-4x3) +x4 -x6
N(x) = x3 + 2x5 -x4 +x2 -2x3 +x-1
= -1+x+x2+(x3- 2x3) -x4+ 2x5
= -1+ x+ x2+ (-x3) -x4+ 2x5
b. M(x) +N(x)= (- 5 +x2 -4x3 +x4 -x6) + (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1+ x+ x2 -x3 -x4+ 2x5
= (-5-1) + x +( x2 +x2) +(-4x3-x3) +(x4-x4) +2x5 -x6
= -6 +x +2x2 +(-5x3) +0 +2x5-x6
= -6 +x +2x2 +(-5x3) +2x5-x6
M(x) -N(x)= (- 5 +x2 -4x3 +x4 -x6) - (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1-x -x2 +x3 +x4 -2x5
= (-5-1) +x +(x2-x2) +(-4x3+x3) +(x4+x4) -2x5 -x6
= -6 +x +0 +(-3x3) +2x4 -2x5 -x6
= -6 +x +(-3x3) +2x4 -2x5 -x6
a. M(x) = 3x2- 5+ x4- 3x3- x6- 2x2- x3
= - 5+ (3x2- 2x2)+(-3x3- x3)+ x4- x6
= - 5 +x2+ (-4x3) +x4 -x6
N(x) = x3 + 2x5 -x4 +x2 -2x3 +x-1
= -1+x+x2+(x3- 2x3) -x4+ 2x5
= -1+ x+ x2+ (-x3) -x4+ 2x5
b. M(x) +N(x)= (- 5 +x2 -4x3 +x4 -x6) + (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1+ x+ x2 -x3 -x4+ 2x5
= (-5-1) + x +( x2 +x2) +(-4x3-x3) +(x4-x4) +2x5 -x6
= -6 +x +2x2 +(-5x3) +0 +2x5-x6
= -6 +x +2x2 +(-5x3) +2x5-x6
M(x) -N(x)= (- 5 +x2 -4x3 +x4 -x6) - (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1-x -x2 +x3 +x4 -2x5
= (-5-1) +x +(x2-x2) +(-4x3+x3) +(x4+x4) -2x5 -x6
= -6 +x +0 +(-3x3) +2x4 -2x5 -x6
= -6 +x +(-3x3) +2x4 -2x5 -x6
Ta đặt và thực hiện phép tính P(x) + Q(x) và P(x) – Q(x) có
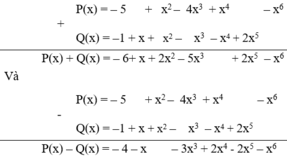
Vậy: P(x) + Q(x) = – 6 + x + 2x2 – 5x3 + 2x5 – x6
P(x) – Q(x) = – 4 – x – 3x3 + 2x4 - 2x5 – x6
a) \(...=P\left(x\right)=2x^4-x^4+3x^3+4x^2-3x^2+3x-x+3\)
\(P\left(x\right)=x^4+3x^3+x^2+2x+3\)
\(...=Q\left(x\right)=x^4+x^3+3x^2-x^2+4x+4-2\)
\(Q\left(x\right)=x^4+x^3+2x^2+4x+2\)
b) \(P\left(x\right)+Q\left(x\right)=\left(x^4+3x^3+x^2+2x+3\right)+\left(x^4+x^3+2x^2+4x+2\right)\)
\(\Rightarrow P\left(x\right)+Q\left(x\right)=2x^4+4x^3+3x^2+6x+5\)
\(P\left(x\right)-Q\left(x\right)=\left(x^4+3x^3+x^2+2x+3\right)-\left(x^4+x^3+2x^2+4x+2\right)\)
\(\)\(\Rightarrow P\left(x\right)-Q\left(x\right)=x^4+3x^3+x^2+2x+3-x^4-x^3-2x^2-4x-2\)
\(\Rightarrow P\left(x\right)-Q\left(x\right)=2x^3-x^2-2x+1\)
`@` `\text {Ans}`
`\downarrow`
`a)`
\(P(x) = 5x^3 + 3 - 3x^2 + x^4 - 2x - 2 + 2x^2 + x\)
`= x^4 + 5x^3 + (-3x^2 + 2x^2) + (-2x+x) + (3-2)`
`= x^4 + 5x^3 - x^2 - x + 1`
\(Q(x) = 2x^4 + x^2 + 2x + 2 - 3x^2 - 5x + 2x^3 - x^4\)
`= (2x^4 - x^4) + 2x^3 + (x^2 - 3x^2) + (2x-5x) + 2`
`= x^4 + 2x^3 - 2x^2 - 3x +2`
`b)`
`P(x)+Q(x) = (x^4 + 5x^3 - x^2 - x + 1) + (x^4 + 2x^3 - 2x^2 - 3x +2)`
`= x^4 + 5x^3 - x^2 - x + 1 + x^4 + 2x^3 - 2x^2 - 3x +2`
`= (x^4+x^4)+(5x^3 + 2x^3) + (-x^2 - 2x^2) + (-x-3x) + (1+2)`
`= 2x^4 + 7x^3 - 3x^2 - 4x + 3`
`P(x)-Q(x)=(x^4 + 5x^3 - x^2 - x + 1) - (x^4 + 2x^3 - 2x^2 - 3x +2)`
`= x^4 + 5x^3 - x^2 - x + 1 - x^4 - 2x^3 + 2x^2 + 3x -2`
`= (x^4 - x^4) + (5x^3 - 2x^3) + (-x^2+2x^2)+(-x+3x)+(1-2)`
`= 3x^3 + x^2 + 2x - 1`
`Q(x)-P(x) = (x^4 + 2x^3 - 2x^2 - 3x +2)-(x^4 + 5x^3 - x^2 - x + 1)`
`= x^4 + 2x^3 - 2x^2 - 3x +2-x^4 - 5x^3 + x^2 + x - 1`
`= (x^4-x^4)+(2x^3 - 5x^3)+(-2x^2+x^2)+(-3x+x)+(2-1)`
`= -3x^3 - x^2 - 2x + 1`
`@` `\text {Kaizuu lv u.}`
P(x) = 3x2 – 5 + x4 – 3x3 – x6 – 2x2 – x3
= – x6 + x4 + (– 3x3 – x3) + (3x2 – 2x2) – 5
= – x6 + x4 – 4x3 + x2 – 5.
= – 5+ x2 – 4x3 + x4 – x6
Và Q(x) = x3 + 2x5 – x4 + x2 – 2x3 + x –1
= 2x5 – x4 + (x3 – 2x3) + x2 + x –1
= 2x5 – x4 – x3 + x2 + x –1.
= –1+ x + x2 – x3 – x4 + 2x5