Giải bất phương trình -2x + 3 > 0 và biểu diễn trên trục số tập nghiệm của nó
Từ đó hãy chỉ ra các khoảng mà nếu x lấy giá trị trong đó thì nhị thức f(x) = -2x + 3 có giá trị
Trái dấu với hệ số của x;
Cùng dấu với hệ số của x.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 7 2023
1:
a: 2x-3=5
=>2x=8
=>x=4
b: (x+2)(3x-15)=0
=>(x-5)(x+2)=0
=>x=5 hoặc x=-2
2:
b: 3x-4<5x-6
=>-2x<-2
=>x>1
HP
31 tháng 8 2021
b, ĐK: \(x\ne8\)
\(A=\dfrac{x-5}{x-8}>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-5>0\\x-8>0\end{matrix}\right.\\\left\{{}\begin{matrix}x-5< 0\\x-8< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>5\\x>8\end{matrix}\right.\\\left\{{}\begin{matrix}x< 5\\x< 8\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x>8\\x< 5\end{matrix}\right.\)
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Dựa vào đồ thị ta thấy hàm số đã cho vô nghiệm
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 2} \right) = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
b) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = 1\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 1} \right) = 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
c) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 1;{x_2} = 3\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).3 = 16 > 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
Đồ thị nằm trên trục hoành với mọi \(x \in \left( { - 1,3} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
d) Dựa vào đồ thị ta thấy hàm số bậc hai đã cho vô nghiệm
Biệt thức \(\Delta = {6^2} - 4.1.10 = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi \(x\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
e) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = - 3\)
Biệt thức \(\Delta = {6^2} - 4.1.9 = 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
g) ) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 4;{x_2} = - 2\)
Biệt thức \(\Delta = {6^2} - 4.1.8 = 4 > 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)
Đồ thị nằm dưới trục hoành với mọi \(x \in \left( { - 4, - 2} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)
CM
29 tháng 8 2019
a) Ta có: 2. (-2) ≤ 3 nên -2 có là nghiệm của bất phương trình
+) 
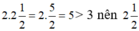không là nghiệm của bất phương trình ,
+) 2π > 3 nên π không là nghiệm của bất phương trình.
+) 
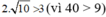nên √10 không là nghiệm của bất phương trình,
Các số là nghiệm của bất phương trình trên là: -2;
Các số không là nghiệm của bất phương trình trên là: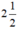 
; π; √10
b)2x ≤ 3 ⇔ x ≤ 3/2
Biểu diễn tập nghiệm trên trục số là:
7 tháng 5 2015
a,A=2x-5 không âm hay 2x-5>0
=> 2x>5
=> x>5/2
Vậy gt của x là 5/2
b, x-8 >= 2.(x+1/2)+7
=> x-8>=2x+1+7
=> x-8>=2x+8
=> -x>=16
=> x=<-16
vậy bpt có tập nghiệm {xlx=<-16}
biểu diễn tập nghiệm trên trục số: (mk vẽ k đk ẹp)
K
0
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Bước 1: Vẽ đường thẳng \(d_1: y-2x=2\) đi qua (0;2) và (-1;0).
Lấy điểm O(0;0) không thuộc \(d_1\). Vì 0-2.0=0<2 nên O thuộc miền nghiệm
Miền nghiệm của BPT \(y - 2x \le 2\) là nửa mp bờ \(d_1\), chứa điểm O.
Bước 2: Vẽ đường thẳng \(d_2: y=4\) đi qua (0;4) và (1;4).
Lấy điểm O(0;0) không thuộc \(d_2\). Vì 0<4 nên O thuộc miền nghiệm.
Miền nghiệm của BPT \(y \le 4\) là nửa mp bờ \(d_2\), chứa điểm O.
Bước 3: Vẽ đường thẳng \(d_3: x=5\) đi qua (5;0) và (5;1).
Lấy điểm O(0;0) không thuộc \(d_3\). Vì 0<5 nên O thuộc miền nghiệm
Miền nghiệm của BPT \(x \le 5\) là nửa mp bờ \(d_3\), chứa điểm O.
Bước 4: Vẽ đường thẳng \(d_4: x + y = - 1\) đi qua (-1;0) và (0;-1).
Lấy điểm O(0;0) không thuộc \(d_4\). Vì 0+0=0>-1 nên O thuộc miền nghiệm.
Miền nghiệm của BPT \(x + y \ge - 1\) là nửa mp bờ \(d_4\), chứa điểm O.
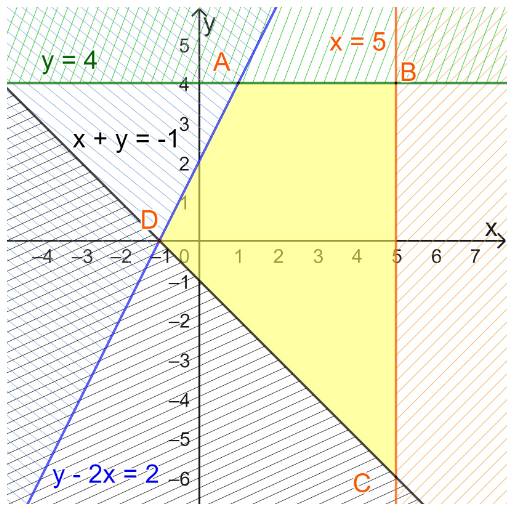
Miền biểu diễn nghiệm của hệ bất phương trình là miền tứ giác ABCD với
A(1;4); B(5;4), C(5;-6); D(-1;0).
Giá trị F tại các điểm A, B, C, D lần lượt là:
\(F\left( {1;4} \right) = - 1 - 4 = - 5\)
\(F\left( {5;4} \right) = - 5 - 4 = - 9\)
\(F\left( {5;-6} \right) = - 5 - (-6) = 1\)
\(F\left( { - 1;0} \right) = - \left( { - 1} \right) - 0 = 1\)
Vậy giá trị lớn nhất của biểu thức F(x;y) là 1 và giá trị nhỏ nhất của biểu thức F(x;y) là -9.
-2x + 3 > 0 ⇔ -2x > -3 ⇔ x < 3/2
Biểu diễn tập nghiệm trên trục số:
Nhị thức f(x) = -2x + 3 có giá trị:
Trái dấu với hệ số của x khi x < 3/2
Cùng dấu với hệ số của x khi x > 3/2