Xét dấu biểu thức: f(x) = (-3x - 3)(x + 2)(x + 3)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 1
\(f\left(x;y\right)=3x^2+y^2-2x-xy+y+3\)
\(=\left(x^2-xy+\dfrac{y^2}{4}\right)+\dfrac{1}{2}\left(4x^2-4x+1\right)+\dfrac{1}{3}\left(\dfrac{9}{4}y^2+3y+1\right)+\dfrac{13}{6}\)
\(=\left(x-\dfrac{y}{2}\right)^2+\dfrac{1}{2}\left(2x-1\right)^2+\dfrac{1}{3}\left(\dfrac{3y}{4}+1\right)^2+\dfrac{13}{6}>0;\forall x;y\)
PT
1
PT
1
NH
0
6 tháng 2 2021
a, \(Chof\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)
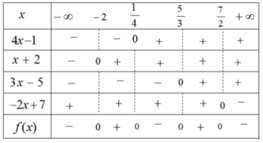
- Lập bảng xét dấu :
Vậy \(\left\{{}\begin{matrix}f\left(x\right)>0\Leftrightarrow x\in\left(3;4\right)\\f\left(x\right)< 0\Leftrightarrow x\in\left(-\infty;3\right)\cup\left(4;+\infty\right)\\f\left(x\right)=0\Leftrightarrow x\in\left\{3;4\right\}\end{matrix}\right.\)
b, \(f\left(x\right)=\left(x-1\right)\left(x+6\right)\)
( Làm tương tự câu a )
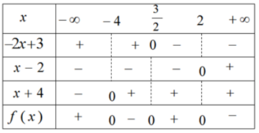
Nhị thức –3x – 3 có nghiệm là –1; nhị thức x + 2 có nghiệm là –2 ; nhị thức x + 3 có nghiệm là –3.
Ta có bảng xét dấu :
Kết luận :
+ f(x) < 0 khi –3 < x < –2 hoặc x > –1
+ f(x) > 0 khi x < –3 hoặc –2 < x < –1.
+ f(x) = 0 khi x = –3 hoặc x = –2 hoặc x = –1.