Cho hình chữ nhật ABCD, AC và BD cắt nhau tại I. Gọi H, K, L, J lần lượt là trung điểm của AD, BC, KC và IC. Chứng minh rằng hai hình thang JLKI và IHDC đồng dạng với nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

31 tháng 8 2019
a) Ta có:
+) M là trung điểm của AD và MN // CD
MN là đường trung bình của hình thang ABCD
N là trung điểm của BC
+) M là trung điểm của AB và ME // AB
ME là đường trung...

28 tháng 9 2019
Gọi H là trung điểm DC.
Chứng minh HE// IF( vì cùng //BC)
=> HE vuông FK ( vì FK vuông IF)
Tương tự HF// EI( vì cùng //AD)
=> HF vuông EK( vì EK vuông IE)
Xét tam giác EFH có EK và FK là 2 đường cao nên K là trực tâm. Suy ra HK vuông FE mà FE //DC nên HK vuông DC tại H suy ra tam giác KDC cân tại K. Nên KD=KC
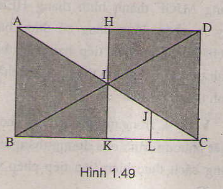
+ I là trung điểm AC; BD; HK
⇒ ĐI(H) = K ; ĐI(D) = B ; ĐI (C) = A.
⇒ Hình thang IKBA đối xứng với hình thang IHDC qua I (1)
+ J; L; K; I lần lượt là trung điểm của CI; CK; CB; CA
⇒ Hình thang JLKI là ảnh của hình thang IKBA qua phép vị tự tâm C tỉ số 1/2.
⇒ Hình thang JLKI là ảnh của hình thang IHDC qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng tâm I và phép vị tự tâm C tỉ số 1/2.
⇒ IJKI và IHDC đồng dạng.