Tìm a và b để các cực trị của hàm số y = 5 3 a 2 x 3 + 2 a x 2 - 9 x + b đều là nhưng số dương và x o = - 5 9 là điểm cực đại.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VD
23 tháng 4 2016
a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)
Q
31 tháng 3 2017
- Xét a = 0 hàm số trở thành y = -9x + b. Trường hợp này hàm số không có cực trị.
- Xét a # 0. Ta có : y’ = 5a2x2 + 4ax – 9 ; y’= 0 ⇔ hoặc
- Với a < 0 ta có bảng biến thiên :
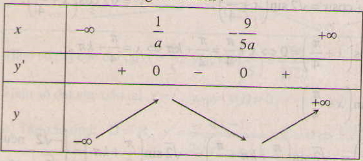
Theo giả thiết là điểm cực đại nên
. Theo yêu cầu bài toán thì
- Với a > 0 ta có bảng biến thiên :
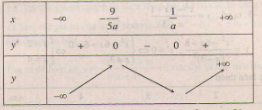
Vì là điểm cực đại nên
. Theo yêu cầu bài toán thì:
Vậy các giá trị a, b cần tìm là: hoặc
.
CM
25 tháng 10 2018
Đáp án B
Ta có y ' = 3 a x 2 + 2 a − 1 x − 3 và y ' ' = 6 a x + 2 a − 2 ; ∀ x ∈ ℝ .
Điểm x 0 = − 1 là điểm cực đại của hàm số ⇔ y ' − 1 = 0 y ' ' − 1 < 0 ⇔ 3 a − 2 a − 1 − 3 = 0 − 6 a + 2 a − 2 < 0 ⇔ a = 1.
Khi đó, hàm số đã cho trở thành y = x 3 − 3 x + b . Ta có y ' = 0 ⇔ 3 x 2 − 3 = 0 ⇔ x = ± 1
Yêu cầu bài toán trở thành y ± 1 > 0 ⇔ b − 2 > 0 b + 2 > 0 ⇔ b > 2.
Vậy a = 1 b > 2 .
10 tháng 4 2018
b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
10 tháng 4 2018
b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
K
5 tháng 8 2020
Ta có \(y'=x^2-x\left(sina+cosa\right)+\frac{3}{4}sin2a\)
Để y có cực đại và cực tiểu thì y' đổi dấu hai lần, tức là:
\(\Delta=\left(sina+cosa\right)^2-3sin2a>0\)
\(\Leftrightarrow1+sin2a-3sin2a>0\)
\(\Leftrightarrow sin2a< \frac{1}{2}\)
\(\Leftrightarrow\frac{5\eta}{6}+k2\eta< 2a< \frac{13\eta}{6}+k2\eta\)
\(\Leftrightarrow\frac{5\eta}{12}+k\eta< a< \frac{13\eta}{12}+k\eta\)
K
5 tháng 8 2020
Tại cực trị \(y'=0\Leftrightarrow x^2-x\left(sina+cosa\right)+\frac{3}{4}sin2a=0\)(*)
(*) cho ta\(x_1+x_2=sina+cosa,x_1x_2=\frac{3}{4}sin2a\)(*)
Để \(x_1+x_2=x^2_1+x^2_2\)thì \(x_1+x_2=\left(x_1+x_2\right)^2-2x_1+x_2\)
\(\Leftrightarrow sina+cosa=\left(sina+cosa\right)^2-\frac{3}{2}sin2a\)
\(\Leftrightarrow sina+cosa=1-\frac{1}{2}sin2a\)
Đặt \(t=cosa+sina=\sqrt{2}cos\left(a-\frac{\eta}{4}\right),t\in\left[-\sqrt{2},\sqrt{2}\right]\)
\(t^2=1+sin2a\Rightarrow sin2a=t^2-1\)
Do đó phương trình trên trở thành:
\(t=1-\frac{1}{2}\left(t^2-1\right)\Leftrightarrow2t=3-t^2\)
\(\Leftrightarrow t^2+2t-3=0\Leftrightarrow t=1,t=-3\)
Vì\(t\in\left[-\sqrt{2},\sqrt{2}\right]\)nên chỉ nhân t=1
\(\Rightarrow cos\left(a-\frac{\eta}{4}\right)=\frac{\sqrt{2}}{2}=cos\frac{\eta}{4}\)
\(\Leftrightarrow a-\frac{\eta}{4}=\pm\frac{\eta}{4}+k2\eta\)
\(\Leftrightarrow a=k2\eta\)hay \(a=\frac{\eta}{2}+k2\eta\)(thỏa điều kiện câu a)
TXĐ: D = R.
Các cực trị của hàm số đều dương
Các cực trị của hàm số đều dương
Vậy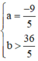
hoặc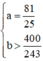 
là các giá trị cần tìm.