Định nghĩa sự đơn điệu ( đồng biến, nghịch biến) của một hàm số trên một khoảng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
1
CM
31 tháng 7 2018
y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
y′ = –3( m 2 + 5m) x 2 + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+)
m
2
+ 5m = 0 ⇔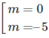 
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với m 2 + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
∆ ' = 36 m 2 + 18( m 2 + 5m) ≤ 0 ⇔ 3 m 2 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( m 2 + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.
8 tháng 9 2021
Trên \(\left(-\dfrac{\pi}{2}+k.2\pi;\dfrac{\pi}{2}+k.2\pi\right)\) chọn 2 giá trị của x (x1 và x2) sao cho x1 > x2
Xét f(x1) - f(x2) = sinx1 - sinx2
= 2cos\(\dfrac{x_1+x_2}{2}\) . sin \(\dfrac{x_1-x_2}{2}\)
Do \(\dfrac{x_1+x_2}{2}\in\left(0;\dfrac{\pi}{2}\right)\)
⇒ cos\(\dfrac{x_1+x_2}{2}\) > 0
Mà \(sin\dfrac{x_1-x_2}{2}\) > 0
nên f(x1) - f(x2) > 0
Vậy đồng biến
Nghịch biến tương tự
8 tháng 9 2021
tại sao \(\dfrac{x_1+x_2}{2}\in\left(0;\dfrac{\pi}{2}\right)\)ạ ?
CM
31 tháng 12 2017
- Điều kiện đồng biến, nghịch biến của hàm số:
Cho hàm số y = f(x) có đạo hàm trên khoảng K.
+ f(x) đồng biến (tăng) trên K nếu f’(x) > 0 với ∀ x ∈ K.
+ f(x) nghịch biến (giảm) trên K nếu f’(x) < 0 với ∀ x ∈ K.
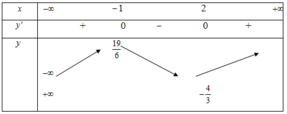
- Xét hàm số
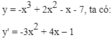
+ Hàm số đồng biến
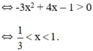
+ Hàm số nghịch biến
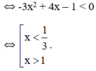
Vậy hàm số đồng biến trên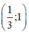 
nghịch biến trên các khoảng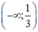 
và (1; +∞)
- Xét hàm số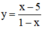 
Ta có: D = R \ {1}
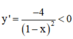∀ x ∈ D.
⇒ Hàm số nghịch biến trên từng khoảng (-∞; 1) và (1; +∞).
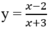
Cho hàm số y = f(x) xác định trên khoảng K, hàm số f(x) được gọi là
Hàm số chỉ đồng biến hoặc nghịch biến trên K gọi là đơn điệu trên K