Một hòn bi A được thả không vận tốc đầu từ đỉnh A của một máng nghiêng AB dài 1m. Hòn bi lăn nhanh dần đều xuống với gia tốc 0,2m/s2. Đồng thời với việc thả hòn bi A, người ta bắn một hòn bi B từ chân dốc B đi lên với vận tốc ban đầu 1m/s. Hòn bi B lăn chậm đều lên dốc cũng với gia tốc 0,2m/s2.a) Viết phương trình tọa độ của hai hòn bi. Lấy gốc tọa độ tại điểm A, chiều...
Đọc tiếp
Một hòn bi A được thả không vận tốc đầu từ đỉnh A của một máng nghiêng AB dài 1m. Hòn bi lăn nhanh dần đều xuống với gia tốc 0,2m/s2. Đồng thời với việc thả hòn bi A, người ta bắn một hòn bi B từ chân dốc B đi lên với vận tốc ban đầu 1m/s. Hòn bi B lăn chậm đều lên dốc cũng với gia tốc 0,2m/s2.
a) Viết phương trình tọa độ của hai hòn bi. Lấy gốc tọa độ tại điểm A, chiều dương hướng dọc theo dốc xuống phía dưới, gốc thời gian là lúc các hòn bi bắt đầu chuyển động.
b) Nếu không va chạm nhau thì hong bi A lăn hết dốc trong thời gian bao lâu? Hòn bi B có thể lên đến đỉnh dốc được không?
c)Xác định thời gian và địa điểm hai hòn bi gặp nhau.
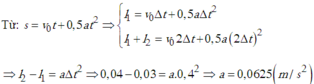
a) Phương trình tọa độ: * Bi A: x 1 = 0 , 1 t 2 (m).
* Bi B: x 2 = 1 − t + 0 , 1 t 2 (m).
b) Khi lăn đến B, tọa độ của bi A là x 1 = 1 m. Ta có: 0 , 1 t 2 = 1 ⇒ t = 10 s.
Nếu coi mặt phẳng nghiêng là đủ dài để bi 2 chuyển động thì quãng đường dài nhất mà 2 bi có thể lăn được cho đến khi dừng v = 0 :
Từ công thức v 2 − v 0 2 = 2 a s ⇒ s m a x = v 2 − v 0 2 2 a = 0 − 1 2 2.0 , 2 = − 2.5 m.
Ta thấy s m a x > A B nên bi 2 có thể lên đỉnh mặt nghiêng.
c) Khi hai hòn bi gặp nhau thì x 1 = x 2 ⇔ 0 , 1 t 2 = 1 − t + 0 , 1 t 2 ⇒ t = 1 s.
Tọa độ gặp nhau: x 1 = x 2 = 0 , 1.1 2 = 0 , 1 m.