Một lăng kính có tiết diện thẳng là một tam giác đều, chiết suất n = 2 , đặt trong không khí (chiết suất n 0 = 1 ). Chiếu một tia sáng đơn sắc nằm trong một tiết diện thẳng đến một mặt bên của lăng kính và hướng từ phía đáy lên với góc tới i. Tia ló ra khỏi mặt bên và đối xứng với tia tới qua lăng kính. Tính góc tới i 1 và góc lệch D?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án cần chọn là: A
Ta có sin i 1 = n sin r 1 ⇒ r 1 = 30 0 ⇒ r 2 = 30 0 ⇒ i 2 = 60 0
Góc lệch D = i 1 + i 2 – A = 60 0

Đáp án A.
Vì tia tới vuông góc với mặt huyền nên đi thẳng tới mặt bên thứ nhất với góc tới 45 0 . Lại có sin i g h = 1 / n = 1 / 1 , 5 → i g h = 41 , 80 . Vì i > i g h xảy ra hiện tượng phản xạ toàn phần. Tia phản xạ cũng tới mặt bên với góc tới 45 0 . nó tiếp tục xảy ra hiện tượng phản xạ toàn phần và tới vuông góc với mặt huyền. Nó đi thẳng

a) Góc lệch có giá trị cực tiểu khi: 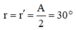
Áp dụng định luật khúc xạ ánh sáng ta có:

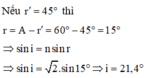
Để tia sáng không ló ra được ở mặt bên thứ 2 thì phải quay lăng kính quanh cạnh lăng kính một góc nhỏ nhất là
![]()

Chọn A
+ Từ hình vẽ ta thấy: i 1 = i 2 = A
+ j 1 = j 2 = 2A
+ j2 = B = 2A
Û 2A = 180 - A 2 ® A = 36 ∘
+ Để có phản xạ toàn phần tại mặt AC thì: i 1 ≥ i gh
Với sin i gh = 1 n ® sin A ≥ 1 n ® n = 1,7

Đáp án B
+ Khi có góc lệch cực tiểu thì i 1 = i 2 = D min + A 2 , r 1 = r 2 = 0 , 5 A .
n = sin D min + A 2 sin A 2 , với D min = A , ta có 3 = sin A sin A 2 → A = 60 °

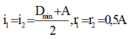
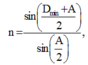
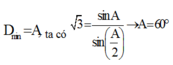
Do tính đối xứng nên: r 1 = r 2 = A 2 = 30 °
Ta có: sin i 1 = n sin r 1 . Thế số: sin i 1 = n sin r 1 = 2 sin 30 0 = 2 2 = > i 1 = 45 0 = i 2
Góc lệch: D = i 1 + i 2 - A = 45 + 45 - 60 = 30 °