Cho tam giác ABC cân tại A, các đường cao AD và BE cắt nhau tại H. Vẽ đường tròn (O) có đường kính AH. Chứng minh rằng: Điểm E nằm trên đường tròn (O).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 9 2017
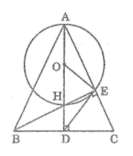
Ta có : OH = OE
Suy ra tam giác OHE cân tại O
Trong tam giác BDH ta có:
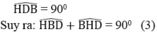
Từ (1), (2) và (3) suy ra:
Tam giác ABC cân tại A có AD ⊥ BC nên BD = CD
Tam giác BCE vuông tại E có ED là đường trung tuyến nên:
ED = DB = BC/2 (tính chất tam giác vuông)
Suy ra tam giác BDE cân tại D
Suy ra: DE ⊥ EO. Vậy DE là tiếp tuyến của đường tròn (O).
3 tháng 8 2018
a/ Xét \(\Delta AEH\)vuông tại E có:
EO là đường trung tuyến ( OA=OH )
\(\Rightarrow EO=\frac{1}{2}AH=OA=OH\)( tính chất đường trung tuyến trong tam giác vuông )
\(\Rightarrow E\)nằm trên đường tròn tâm O đường kính AH
b/ Xét \(\Delta OHE\)có:
OH=OE ( cmt )
\(\Rightarrow\Delta OHE\)cân tại O
\(\Rightarrow\widehat{OEH}=\widehat{OHE}\)( tính chất tam giác cân )
Mà: \(\widehat{BHD}=\widehat{OHE}\)( 2 góc đối đỉnh )
\(\Rightarrow\widehat{OEH}=\widehat{BHD}\left(=\widehat{OHE}\right)\)(1)
Xét \(\Delta ABC\)cân tại A có:
AD là đường cao ( gt )
\(\Rightarrow AD\)là đường trung tuyến
\(\Rightarrow BD=CD\)
Xét \(\Delta BEC\)vuông tại E có:
ED là đường trung tuyến ( BD=CD )
\(\Rightarrow ED=\frac{1}{2}BC=BD\)( tính chất đường trung tuyến trong tam giác vuông )
\(\Rightarrow\Delta BDE\)cân tại D
\(\Rightarrow\widehat{DEH}=\widehat{DBH}\)(2)
Từ (1) và (2) suy ra: \(\widehat{OEH}+\widehat{DEH}=\widehat{BHD}+\widehat{DBH}\)
Hay \(\widehat{OED}=90\)( \(\widehat{BHD}\)và \(\widehat{DBH}\)là 2 góc phụ nhau của \(\Delta BHD\)vuông tại D )
\(\Rightarrow DE\perp OE\)
Vậy DE là tiếp tuyến của đường tròn (O).
10 tháng 8 2017
1.Xét tứ giác CEHD ta có:
Góc CEH = 900 (Vì BE là đường cao)
Góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEC = 900.
CF là đường cao => CF ┴ AB => góc BFC = 900.
Như vậy E và F cùng nhìn BC dưới một góc 900 => E và F cùng nằm trên đường tròn đường kính BC.
Vậy bốn điểm B,C,E,F cùng nằm trên một đường tròn.
3. Xét hai tam giác AEH và ADC ta có: góc AEH = góc ADC = 900; góc A là góc chung
=> Δ AEH ˜ Δ ADC => AE/AD = AH/AC=> AE.AC = AH.AD.
* Xét hai tam giác BEC và ADC ta có: góc BEC = góc ADC = 900; góc C là góc chung
=> Δ BEC ˜ Δ ADC => AE/AD = BC/AC => AD.BC = BE.AC.
4. Ta có góc C1 = góc A1 (vì cùng phụ với góc ABC)
góc C2 = góc A1 ( vì là hai góc nội tiếp cùng chắn cung BM)
=> góc C1 = góc C2 => CB là tia phân giác của góc HCM; lại có CB ┴ HM => Δ CHM cân tại C
=> CB cũng là đương trung trực của HM vậy H và M đối xứng nhau qua BC.
5. Theo chứng minh trên bốn điểm B, C, E, F cùng nằm trên một đường tròn
=> góc C1 = góc E1 (vì là hai góc nội tiếp cùng chắn cung BF)
Cũng theo chứng minh trên CEHD là tứ giác nội tiếp
góc C1 = góc E2 (vì là hai góc nội tiếp cùng chắn cung HD)
góc E1 = góc E2 => EB là tia phân giác của góc FED.
Chứng minh tương tự ta cũng có FC là tia phân giác của góc DFE mà BE và CF cắt nhau tại H do đó H là tâm đường tròn nội tiếp tam giác DEF.
10 tháng 8 2017
1. Xét tứ giác CEHD ta có:
góc CEH = 900 (Vì BE là đường cao)
góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEA = 900.
AD là đường cao => AD ┴ BC => BDA = 900.
Như vậy E và D cùng nhìn AB dưới một góc 900 => E và D cùng nằm trên đường tròn đường kính AB.
Vậy bốn điểm A, E, D, B cùng nằm trên một đường tròn.
3. Theo giả thiết tam giác ABC cân tại A có AD là đường cao nên cũng là đường trung tuyến
=> D là trung điểm của BC. Theo trên ta có góc BEC = 900.
Vậy tam giác BEC vuông tại E có ED là trung tuyến => DE = 1/2 BC.
4. Vì O là tâm đường tròn ngoại tiếp tam giác AHE nên O là trung điểm của AH => OA = OE => tam giác AOE cân tại O => góc E1 = góc A1 (1).
Theo trên DE = 1/2 BC => tam giác DBE cân tại D => góc E3 = góc B1 (2)
Mà góc B1 = góc A1 (vì cùng phụ với góc ACB) => góc E1 = góc E3 => góc E1 + góc E2 = góc E2 + góc E3
Mà góc E1 + góc E2 = góc BEA = 900 => góc E2 + góc E3 = 900 = góc OED => DE ┴ OE tại E.
Vậy DE là tiếp tuyến của đường tròn (O) tại E.
5. Theo giả thiết AH = 6 Cm => OH = OE = 3 cm.; DH = 2 Cm => OD = 5 cm. Áp dụng định lí Pitago cho tam giác OED vuông tại E ta có ED2 = OD2 – OE2 ↔ ED2 = 52 – 32 ↔ ED = 4cm
CM
14 tháng 3 2019
b) Xét tứ giác BFEC có:
∠(BFC) = 90 0 (Do CF là đường cao)
∠(BEC ) = 90 0 (Do BE là đường cao)
⇒ E và F cùng nhìn BC dưới một góc bằng nhau
⇒ Tứ giác BFEC nội tiếp được đường tròn
⇒ Bốn điểm B, E, F, C cùng nằm trên đường tròn
Gọi O là trung điểm của AH
Tam giác AEH vuông tại E có EO là đường trung tuyến nên :
EO = OA = OH = AH/2 (tính chất tam giác vuông)
Vậy điểm E nằm trên đường tròn (O ; AH/2 )