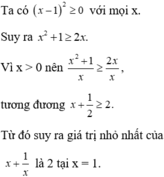Cho x ≥ 2 . Chứng minh x + 1 x ≥ 5 2 . Từ đó tìm giá trị nhỏ nhất của x + 1 x .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



tự biên tự diễn thôi:
a/ gọi 2 số phải tìm là a và b, ta có a+b chia hết cho 3
ta có a^3+b^3=(a+b)(a^2-ab+b^2)=(a+b)[(a^2+2ab+b^2)-3ab]= (a+b)[(a+b)^2-3ab]0,5
vì a+b chia hết cho 3 nên (a+b)^2-3ab chia hết cho 3
do vậy (a+b)[(a+b)^2-3ab] chia hết cho 3
ai làm câu b

\(b,B\left(x\right)=x\left(x-3\right)-2\left(x+5\right)=x^2-3x-2x-10=x^2-5x-10\)
\(=x^2-\frac{5}{2}x-\frac{5}{2}x+\frac{25}{4}-\frac{25}{4}-10=x\left(x-\frac{5}{2}\right)-\frac{5}{2}\left(x-\frac{5}{2}\right)-\frac{65}{4}\)
\(=\left(x-\frac{5}{2}\right)^2-\frac{65}{4}\)
Vì \(\left(x-\frac{5}{2}\right)^2\ge0=>\left(x-\frac{5}{2}\right)^2-\frac{65}{4}\ge-\frac{65}{4}\) (với mọi x)
Dấu "=" xảy ra \(< =>x-\frac{5}{2}=0< =>x=\frac{5}{2}\)
Vậy minB(x)=-65/4 khi x=5/2
\(c,C\left(x\right)=2x\left(x+1\right)-3x\left(x+1\right)=2x^2+2x-3x^2-3x=-x^2-x\)
\(=-\left(x^2+x\right)=-\left(x^2+x+1-1\right)=-\left(x^2+\frac{1}{2}x+\frac{1}{2}x+\frac{1}{4}+\frac{3}{4}-1\right)\)
\(=-\left[x\left(x+\frac{1}{2}\right)+\frac{1}{2}\left(x+\frac{1}{2}\right)-\frac{1}{4}\right]=-\left[\left(x+\frac{1}{2}\right)^2-\frac{1}{4}\right]=\frac{1}{4}-\left(x+\frac{1}{2}\right)^2\)
Vì \(\left(x+\frac{1}{2}\right)^2\ge0=>\frac{1}{4}-\left(x+\frac{1}{2}\right)^2\le\frac{1}{4}\) (với mọi x)
Dấu "=" xảy ra \(< =>x+\frac{1}{2}=0< =>x=-\frac{1}{2}\)
Vậy maxC(x)=1/4 khi x=-1/2
\(A\left(x\right)=2x\left(x-1\right)-3\left(x-13\right)=2x^2-5x+39\)
\(=2\left(x^2-\frac{5}{2}x+\frac{39}{2}\right)=2\left(x^2-\frac{5}{4}x-\frac{5}{4}x+\frac{25}{16}-\frac{25}{16}+\frac{39}{2}\right)\)
\(=2\left[x\left(x-\frac{5}{4}\right)-\frac{5}{4}\left(x-\frac{5}{4}\right)\right]+\frac{287}{16}=2\left[\left(x-\frac{5}{4}\right)^2+\frac{287}{16}\right]=2\left(x-\frac{5}{4}\right)^2+\frac{287}{8}\)
Vì \(2\left(x-\frac{5}{4}\right)^2\ge0=>2\left(x-\frac{5}{4}\right)^2+\frac{287}{8}\ge\frac{287}{8}>0\) với mọi x
=>A(x) vô nghiệm (đpcm)

\(A=x^2+3x-5=x^2+3x+\frac{9}{4}-\frac{29}{4}\)
\(=\left(x+\frac{3}{2}\right)^2-\frac{29}{4}\ge-\frac{29}{4}\)
Vậy \(A_{min}=-\frac{29}{4}\Leftrightarrow x+\frac{3}{2}=0\Leftrightarrow x=-\frac{3}{2}\)

bài 2
Ta có:
\(A=\left|x-102\right|+\left|2-x\right|\Rightarrow A\ge\left|x-102+2-x\right|=-100\Rightarrow GTNNcủaAlà-100\)đạt được khi \(\left|x-102\right|.\left|2-x\right|=0\)
Trường hợp 1: \(x-102>0\Rightarrow x>102\)
\(2-x>0\Rightarrow x< 2\)
\(\Rightarrow102< x< 2\left(loại\right)\)
Trường hợp 2:\(x-102< 0\Rightarrow x< 102\)
\(2-x< 0\Rightarrow x>2\)
\(\Rightarrow2< x< 102\left(nhận\right)\)
Vậy GTNN của A là -100 đạt được khi 2<x<102.

1. a, => -12x+60+21-7x = 5
=> 81 - 19x = 5
=> 19x = 81 - 5 = 76
=> x = 76 : 19 = 4
Tk mk nha

a: \(A=\dfrac{x^2+2+x^2-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2-x}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x}{x^2+x+1}\)