Rút gọn rồi tính giá trị các biểu thức sau: - 9 a - 9 + 12 a + 4 a 2 t ạ i a = - 9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 5 2021
a)
√
−
9
a
−
√
9
+
12
a
+
4
a
2
=
√
−
9
a
−
√
3
2
+
2.3
.2
a
+
(
2
a
)
2
=
√
3
2
⋅
(
−
a
)
−
√
(
3
+
2
a
)
2
=
3
√
−
a
−
|
3
+
2
a
|
Thay
a
=
−
9
ta được:
3
√
9
−
|
3
+
2
⋅
(
−
9
)
|
=
3.3
−
15
=
−
6
.
b) Điều kiện:
m
≠
2
1
+
3
m
m
−
2
√
m
2
−
4
m
+
4
=
1
+
3
m
m
−
2
√
m
2
−
2.2
⋅
m
+
2
2
=
1
+
3
m
m
−
2
√
(
m
−
2
)
2
=
1
+
3
m
|
m
−
2
|
m
−
2
+)
m
>
2
, ta được:
1
+
3
m
m
−
2
√
m
2
−
4
m
+
4
=
1
+
3
m
.
(
1
)
+)
m
<
2
, ta được:
1
+
3
m
m
−
2
√
m
2
−
4
m
+
4
=
1
−
3
m
.
(
2
)
Với
m
=
1
,
5
<
2
. Thay vào biểu thức
(
2
)
ta có:
1
−
3
m
=
1
−
3.1
,
5
=
−
3
,
5
Vậy giá trị biểu thức tại
m
=
1
,
5
là
−
3
,
5
.
c)
√
1
−
10
a
+
25
a
2
−
4
a
=
√
1
−
2.1
.5
a
+
(
5
a
)
2
−
4
a
=
√
(
1
−
5
a
)
2
−
4
a
=
|
1
−
5
a
|
−
4
a
+) Với
a
<
1
5
, ta được:
1
−
5
a
−
4
a
=
1
−
9
a
.
(
3
)
+) Với
a
≥
1
5
, ta được:
5
a
−
1
−
4
a
=
a
−
1
.
(
4
)
Vì
a
=
√
2
>
1
5
. Thay vào biểu thức
(
4
)
ta có:
a
−
1
=
√
2
−
1
.
Vậy giá trị của biểu thức tại
a
=
√
2
là
√
2
−
1
.
d)
4
x
−
√
9
x
2
+
6
x
+
1
=
4
x
−
√
(
3
x
)
2
+
2.3
x
+
1
=
4
x
−
√
(
3
x
+
1
)
2
=
4
x
−
|
3
x
+
1
|
+) Với
3
x
+
1
≥
0
⇔
x
≥
−
1
3
, ta có:
4
x
−
(
3
x
+
1
)
=
4
x
−
3
x
−
1
=
x
−
1
.
(
5
)
+) Với
3
x
+
1
<
0
⇔
x
<
−
1
3
, ta có:
4
x
+
(
3
x
+
1
)
=
4
x
+
3
x
+
1
=
7
x
+
1
.
(
6
)
Vì
x
=
−
√
3
<
−
1
3
. Thay vào biểu thức
(
6
)
, ta có:
7
x
+
1
=
7
.
(
−
√
3
)
+
1
=
−
7
√
3
+
1
.
Giá trị của biểu thức tại
x
=
−
√
3
là
−
7
√
3
+
1
19 tháng 5 2021
a) \sqrt{-9a}-\sqrt{9+12 a+4 a^{2}}−9a−9+12a+4a2
=\sqrt{-9 a}-\sqrt{3^{2}+2.3 .2 a+(2 a)^{2}}=−9a−32+2.3.2a+(2a)2
=\sqrt{3^{2} \cdot(-a)}-\sqrt{(3+2 a)^{2}}=32⋅(−a)−(3+2a)2
=3 \sqrt{-a}-|3+2 a|=3−a−∣3+2a∣
Thay a=-9a=−9 ta được:
3 \sqrt{9}-|3+2 \cdot(-9)|=3.3-15=-639−∣3+2⋅(−9)∣=3.3−15=−6.
b) Điều kiện: m \neq 2m=2
1+\dfrac{3 m}{m-2} \sqrt{m^{2}-4 m+4}1+m−23mm2−4m+4
=1+\dfrac{3 m}{m-2} \sqrt{m^{2}-2.2 \cdot m+2^{2}}=1+m−23mm2−2.2⋅m+22
=1+\dfrac{3 m}{m-2} \sqrt{(m-2)^{2}}=1+m−23m(m−2)2
=1+\dfrac{3 m|m-2|}{m-2}=1+m−23m∣m−2∣
+) m>2m>2, ta được: 1+\dfrac{3 m}{m-2} \sqrt{m^{2}-4 m+4}=1+3 m1+m−23mm2−4m+4=1+3m. (1)(1)
+) m<2m<2, ta được: 1+\dfrac{3 m}{m-2} \sqrt{m^{2}-4 m+4}=1-3 m1+m−23mm2−4m+4=1−3m. (2)(2)
Với m=1,5<2m=1,5<2. Thay vào biểu thức (2)(2) ta có: 1-3 m=1-3.1,5=-3,51−3m=1−3.1,5=−3,5
Vậy giá trị biểu thức tại m=1,5m=1,5 là -3,5−3,5.
c) \sqrt{1-10 a+25 a^{2}}-4a1−10a+25a2−4a
=\sqrt{1-2.1 .5 a+(5 a)^{2}}-4 a=1−2.1.5a+(5a)2−4a
=\sqrt{(1-5a)^{2}}-4 a=(1−5a)2−4a
=|1-5 a|-4 a=∣1−5a∣−4a
+) Với a <\dfrac{1}{5}a<51, ta được: 1-5a-4 a=1-9a1−5a−4a=1−9a. (3)(3)
+) Với a \ge \dfrac{1}{5}a≥51, ta được: 5 a-1-4 a=a-15a−1−4a=a−1. (4)(4)
Vì a=\sqrt{2}>\dfrac{1}{5}a=2>51. Thay vào biểu thức (4)(4) ta có: a-1=\sqrt{2}-1a−1=2−1.
Vậy giá trị của biểu thức tại a=\sqrt{2}a=2 là \sqrt{2}-12−1.
d) 4 x-\sqrt{9 x^{2}+6 x+1}4x−9x2+6x+1
=4 x-\sqrt{(3 x)^{2}+2.3 x+1}=4 x-\sqrt{(3 x+1)^{2}}=4x−(3x)2+2.3x+1=4x−(3x+1)2
=4 x-|3x+1|=4x−∣3x+1∣
+) Với 3x+1 \geq 03x+1≥0 \Leftrightarrow⇔ x \ge -\dfrac{1}{3}x≥−31, ta có: 4 x-(3x+1)=4 x-3 x-1 =x-14x−(3x+1)=4x−3x−1=x−1. (5)(5)
+) Với 3x+1<03x+1<0 \Leftrightarrow⇔ x <-\dfrac{1}{3}x<−31, ta có: 4 x+(3 x+1)=4 x+3x+1=7x+14x+(3x+1)=4x+3x+1=7x+1. (6)(6)
Vì x=-\sqrt{3}<-\dfrac{1}{3}x=−3<−31. Thay vào biểu thức (6)(6), ta có: 7 x+1=7 .(-\sqrt{3})+1=-7 \sqrt{3}+17x+1=7 .(−3)+1=−73+1.
Giá trị của biểu thức tại x=-\sqrt{3}x=−3 là -7 \sqrt{3}+1−73+1.
CM
27 tháng 2 2018
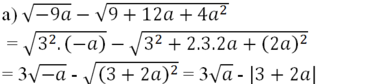
Tại a = -9 ta được:
= 3√-(-9) - |3 + 2(-9)|
= 3√32 - |3 - 18|
= 3.3 - |-15| = 9 - 15 = -6
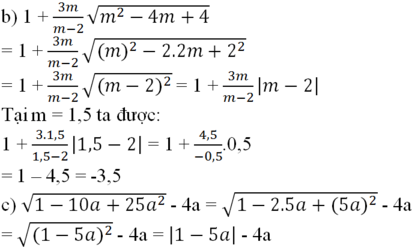
Tại a = √2 ta được:
= |1 - 5√2| - 4√2
= (5√2 - 1) - 4√2
= √2 - 1
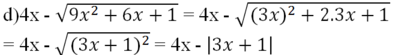
Tại x = -√3 ta được:
= 4(-√3) - |3(-√3) + 1|
= -4√3 - |-3√3 + 1|
= -4√3 - (3√3 - 1)
= -7√3 + 1
31 tháng 12 2023
a: Thay x=49 vào A, ta được:
\(A=\dfrac{2\cdot7+1}{7-3}=\dfrac{14+1}{4}=\dfrac{15}{4}\)
b: \(B=\dfrac{2x+36}{x-9}-\dfrac{9}{\sqrt{x}-3}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(=\dfrac{2x+36}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{9}{\sqrt{x}-3}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(=\dfrac{2x+36-9\left(\sqrt{x}+3\right)-\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2x+36-9\sqrt{x}-27-x+3\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-6\sqrt{x}+9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)^2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)
c: \(P=A\cdot B=\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\cdot\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{2\sqrt{x}+1}{\sqrt{x}+3}\)
P>1 khi P-1>0
=>\(\dfrac{2\sqrt{x}+1-\sqrt{x}-3}{\sqrt{x}+3}>0\)
=>\(\sqrt{x}-2>0\)
=>\(\sqrt{x}>2\)
=>x>4
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}x>4\\x\ne9\end{matrix}\right.\)
3 tháng 5 2022
a. = \(\dfrac{2}{x+5}\)+\(\dfrac{2x+30}{\left(x-5\right)\left(x+5\right)}\)
= 2.(x-5) + 2x+30
= 2x-10+2x+30
=4x+20
b. x=9
4x+20
=4.9+20
=36+20
=56
28 tháng 9 2021
Câu 2:
a: Ta có: \(P=3x-\sqrt{x^2-10x+25}\)
\(=3x-\left|x-5\right|\)
\(=\left[{}\begin{matrix}3x-x+5=2x+5\left(x\ge5\right)\\3x+x-5=4x-5\left(x< 5\right)\end{matrix}\right.\)
b: Vì x=2<5 nên \(P=4\cdot2-5=8-5=3\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2023
1.
\(A=\dfrac{2x-9}{\left(x-2\right)\left(x-3\right)}-\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-2\right)\left(x-3\right)}+\dfrac{\left(2x+4\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{2x-9-\left(x^2-9\right)+\left(2x^2-8\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x^2+2x-8}{\left(x-2\right)\left(x-3\right)}=\dfrac{\left(x-2\right)\left(x+4\right)}{\left(x-2\right)\left(x-3\right)}\)
\(=\dfrac{x+4}{x-3}\)
b.
\(A=2\Rightarrow\dfrac{x+4}{x-3}=2\Rightarrow x+4=2\left(x-3\right)\)
\(\Rightarrow x=10\) (thỏa mãn)
2.
\(x^4+2x^2y+y^2-9=\left(x^2+y\right)^2-3^2=\left(x^2+y-3\right)\left(x^2+y+3\right)\)
TN
3
I
5 tháng 1 2023
\(a,\dfrac{x^2+6x+9}{x+3}\\ đk:x\ne-3\\ =\dfrac{\left(x+3\right)^2}{x+3}=x+3\)
b, Thay \(x=-2\left(t/mđk\right)\) vào
\(-2+3=1\)
Vậy tại \(x=-2\) thì biểu thức = 1
5 tháng 1 2023
\(A=\dfrac{x^2+6x+9}{x+3}\)
\(A=\dfrac{x^2+2.x.3+3^2}{x+3}\)
\(A=\dfrac{\left(x+3\right)^2}{x+3}\)
\(A=x+3\)
b) Thay x = -2 vào A ta được A = -2 + 3 = 1
Vậy khi x = -2 thì A = 1
12 tháng 3 2023
\(A=\dfrac{3-x}{x+3}.\dfrac{x^2+6x+9}{x^2-9}+\dfrac{x}{x+3}\left(ĐKXĐ:x\ne\pm3\right)\)
a, \(A=\dfrac{-\left(x-3\right)\left(x+3\right)^2}{\left(x+3\right)^2\left(x-3\right)}+\dfrac{x}{x+3}\)
\(=-1+\dfrac{x}{x+3}=\dfrac{-x-3+x}{x+3}=\dfrac{-3}{x+3}\)
b, \(x^2-2x-3=0\Leftrightarrow x^2-3x+x-3\Leftrightarrow x\left(x-3\right)+\left(x-3\right)\Leftrightarrow\left(x-3\right)\left(x+1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
TH1 : Nếu x = 3 thì gt của biểu thức \(A=\dfrac{-3}{3+3}=-\dfrac{3}{6}=-\dfrac{1}{2}\)
TH2 : Nếu x = -2 thì gt của biểu thức \(A=\dfrac{-3}{-2+3}=-3\)
c, Để A nhận giá trị nguyên thì \(x+3\inƯ\left(3\right)\) ( Ư(-3 ) cũng được như nhau nhé ! )
Xét bảng :
| x + 3 | x |
| 1 | -2 |
| -1 | -4 |
| 3 | 0 |
| -3 | -6 |
Vậy để A nguyên thì \(x\in\left\{-6;-4;-2;0\right\}\)
Tại a = -9 ta được:
= 3√-(-9) - |3 + 2(-9)|
= 3√32 - |3 - 18|
= 3.3 - |-15| = 9 - 15 = -6