Chứng minh các đẳng thức sau: 2 3 - 6 8 - 2 - 216 3 . 1 6 = - 1 , 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Ta có: \(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-2\sqrt{6}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}}{2}-\dfrac{4\sqrt{6}}{2}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{-3}{2}\)

Biến đổi Vế trái ta có :
\(\left(\frac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\frac{\sqrt{216}}{3}\right)\cdot\frac{1}{\sqrt{6}}\)
\(=\left(\frac{\sqrt{3}\left(2-\sqrt{2}\right)}{\sqrt{2}\left(2-\sqrt{2}\right)}-\frac{3\sqrt{24}}{3}\right)\cdot\frac{1}{\sqrt{6}}\)
\(\left(\frac{\sqrt{3}}{\sqrt{2}}-2\sqrt{6}\right)\cdot\frac{1}{\sqrt{6}}=\frac{\sqrt{3}}{\sqrt{2}}\cdot\frac{1}{\sqrt{6}}-2\sqrt{6}\cdot\frac{1}{\sqrt{6}}\)
\(=\frac{1}{2}-2=-1,5=VP\) ( ĐPCM)
Biến đổi vế trái :
\(VT=\left(\frac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\frac{\sqrt{216}}{3}\right).\frac{1}{\sqrt{6}}\)
\(=\left(\frac{\sqrt{2}.\sqrt{2}.\sqrt{3}-\sqrt{6}}{\sqrt{2^2.2}-2}-\frac{\sqrt{6^2.6}}{3}\right).\frac{1}{\sqrt{6}}\)
\(=\left(\frac{\sqrt{2}.\sqrt{6}-\sqrt{6}}{2\sqrt{2}-2}-\frac{6\sqrt{6}}{3}\right).\frac{1}{\sqrt{6}}\)
\(=\left(\frac{\sqrt{6}.\left(\sqrt{2}-1\right)}{2.\left(\sqrt{2}-1\right)}-2\sqrt{6}\right).\frac{1}{\sqrt{6}}\)
\(=\left(\frac{\sqrt{6}}{2}-2\sqrt{6}\right).\frac{1}{\sqrt{6}}\)
\(=\sqrt{6}.\left(\frac{1}{2}-2\right).\frac{1}{\sqrt{6}}=-\frac{3}{2}=-1,5=VP\left(đpcm\right)\)

\(\left(4-\sqrt{7}\right)^2=4^2-2\cdot4\cdot\sqrt{7}+7\)
\(=16-8\sqrt{7}+7=23-8\sqrt{7}\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}\)
\(=\sqrt{5-2\cdot\sqrt{5}\cdot2+4}-\sqrt{5}\)
\(=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}\)
\(=\left|\sqrt{5}-2\right|-\sqrt{5}\)
\(=\sqrt{5}-2-\sqrt{5}=-2\)
\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}+1}\)
\(=\dfrac{\sqrt{3-2\cdot\sqrt{3}\cdot1+1}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}=\dfrac{3-1}{2-1}=2\)
\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-\dfrac{6\sqrt{6}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{1}{2}\sqrt{6}-2\sqrt{6}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{1}{2}-2=-\dfrac{3}{2}=-1,5\)

\(sin^6a+cos^6a=\left(sin^2x\right)^3+\left(cos^2x\right)^3\)
\(=\left(sin^2x+cos^2x\right)\left(sin^4x+cos^4x-sin^2x.cos^2x\right)\)
\(=sin^4x+2sin^2xcos^2x+cos^4x-3sin^2x.cos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-\frac{3}{4}.\left(2sinx.cosx\right)^2\)
\(=1-\frac{3}{4}sin^22x=1-\frac{3}{4}\left(\frac{1}{2}-\frac{1}{2}cos4x\right)=\frac{5}{8}+\frac{3}{8}cos4x\)
2/
\(\frac{1+sin2a-cos2a}{1+cos2a}=\frac{1+2sina.cosa-\left(1-2sin^2a\right)}{1+2cos^2a-1}=\frac{2sina.cosa+2sin^2a}{2cos^2a}\)
\(=\frac{2sina.cosa}{2cos^2a}+\frac{2sin^2a}{2cos^2a}=tana+tan^2a\)

giả sử 2 vế bằng nhau, nhân tích chéo, rồi được 2 vế = nhau là kết luận thỏa mãn
\(\frac{\sqrt{2}+\sqrt{3}+\sqrt{4}}{\sqrt{2}+\sqrt{3}+\sqrt{4}+\sqrt{2}\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)}=\frac{1}{1+\sqrt{2}}=\frac{\sqrt{2}-1}{2-1}=\sqrt{2}-1=vp\)
Chứng minh các bất đẳng thức:
a) căn 6 - căn 2 >1
b) căn 5 - căn 3>1/2
c) căn 7 - căn 6 < căn 6 - căn 5


tham khảo:
\(a) 2+5+8+...+(3n−1)=n(3n+1)2 (1) Đặt Sn=2+5+8+...+(3n−1) Với n=1 ta có: S1=2=1(3.1+1)2 Giả sử (1) đúng với n=k(k≥1), tức là Sk=2+5+8+...+(3k−1)=k(3k+1)2 Ta chứng minh (1) đúng với n=k+1 hay Sk+1=(k+1)(3k+4)2 Thật vậy ta có: Sk+1=2+5+8+...+(3k−1)+[3(k+1)−1]=Sk+3k+2=k(3k+1)2+3k+2=3k2+k+6k+42=3k2+7k+42=(k+1)(3k+4)2 Vậy (1) đúng với mọi k≥1 hay (1) đúng với mọi n∈N∗ b) 3+9+27+...+3n=12(3n+1−3) (2) Đặt Sn=3+9+27+...+3n=12(3n+1−3) Với n=1, ta có: S1=3=12(32−3) (hệ thức đúng) Giả sử (2) đúng với n=k(k≥1) tức là Sk=3+9+27+...+3k=12(3k+1−3) Ta chứng minh (2) đúng với n=k+1, tức là chứng minh Sk+1=12(3k+2−3) Thật vậy, ta có: Sk+1=3+9+27+...+3k+1=Sk+3k+1=12(3k+1−3)+3k+1=32.3k+1−32=12(3k+2−3)(đpcm) Vậy (2) đúng với mọi k≥1 hay đúng với mọi n∈N∗\)
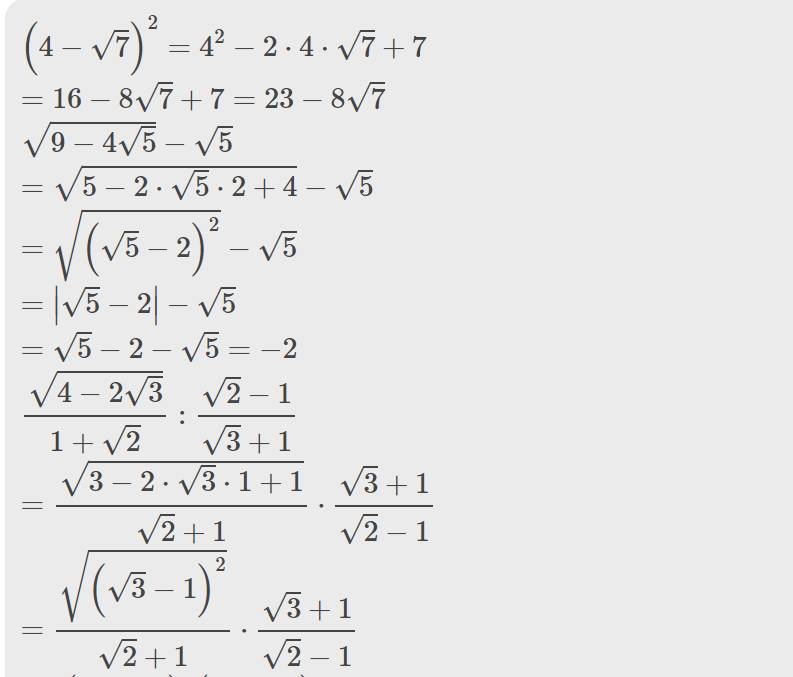
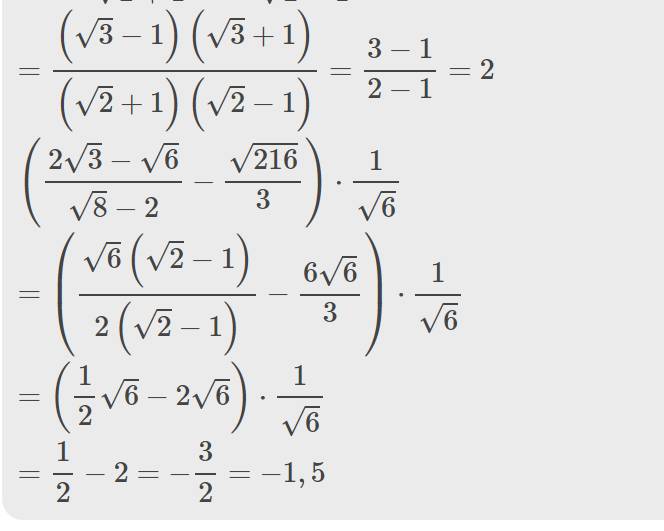
Biến đổi vế trái: