Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm.
Tính khoảng cách từ tâm O đến dây AB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

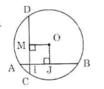
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra: J là trung điểm của AB.
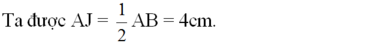
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 (OA = R = 5cm)
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.
b) Kẻ OM vuông góc với CD tại M.
Tứ giác OJIM có: 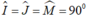 nên là hình chữ nhật
nên là hình chữ nhật
Ta có IJ = AJ – AI = 4 – 1 = 3cm
=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)
Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)

 ∆OBH vuông tại H
∆OBH vuông tại H
⇒ OB² = OH² + BH² (Pytago)
⇒ BH² = OB² - OH²
= 5² - 4²
= 9
⇒ BH = 3 (cm)
Do OH ⊥ AB
⇒ H là trung điểm của AB
⇒ AB = 2BH = 2.3 = 6 (cm)
Gọi OH là khoảng cách từ tâm O đến dây AB
=>OH\(\perp\)AB tại H
=>OH=4cm
ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
ΔOHA vuông tại H
=>\(OH^2+HA^2=OA^2\)
=>\(HA^2+4^2=5^2\)
=>\(HA^2=5^2-4^2=9\)
=>HA=3(cm)
H là trung điểm của AB
=>\(AB=2\cdot AH=6\left(cm\right)\)

Đáp án A
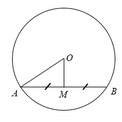
Vì M là trung điểm của AB nên ta có: 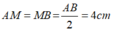
Theo quan hệ vuông góc giữa đường kính và dây ta có:
OM ⊥ AB
Áp dụng định lí Pytago vào tam giác OAM ta có:
O M 2 = O A 2 - A M 2 = 52 - 42 = 9 ⇒ O M = 3 c m

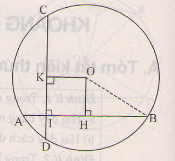
a) Vẽ OH⊥ABOH⊥AB, ta có HA=HB=4cm.
Xét tam giác HOB vuông tại H, có:
OH2=OB2−HB2=52−42=9⇒OH=3(cm)OH2=OB2−HB2=52−42=9⇒OH=3(cm).
b) Vẽ OK⊥CDOK⊥CD. TỨ giác KOHI có ba góc vuông nên là hình chữ nhật, suy ra OK=HI. Ta có HI=4-1=3cm, suy ra OK=3cm.
Vậy OH=OK=3cm.
Hai dây AB và CD cách đều tâm nên chúng bằng nhau.
Do đó AB=CD.
a) Vẽ OH ⊥ AB, ta có HA=HB=4cm.
Xét tam giác HOB vuông tại H, có:
OH2 = OB2 – HB2 =52 – 42 = 9
⇒ OH = 3(cm).
b) Vẽ OK ⊥ CD. Tứ giác KOHI có ba góc vuông nên là hình chữ nhật, suy ra OK=HI.
Ta có HI=4-1=3cm, suy ra OK=3cm.
Vậy OH=OK=3cm. Hai dây AB và CD cách đều tâm nên chúng bằng nhau.
Do đó AB=CD.
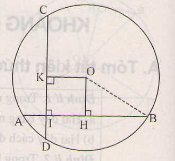

Qua O kẻ đường thẳng vuông góc AB và CD, lần lượt cắt AB và CD tại E và F ⇒ E là trung điểm AB, F là trung điểm CD
AE=12AB=4(cm) ; CF=12CD=3(cm)
Áp dụng định lý pytago cho tam giác vuông OAE
OE=√OA2−AE2=√R2−AE2=3(cm)
Pitago tam giác vuông OCF:
OF=√OC2−CF2=√R2−CF2=4(cm)
⇒EF=OE+OF=7(cm)
chúc bn học tốt !
a) Ta có AH là đường cao của tam giác ABC, do đó AB là đường trung trực của đoạn thẳng LH (vì H là trung điểm của BC).
b) Ta có $\angle AED = \angle ACD$ do cùng chắn cung AD trên đường tròn (T). Mà $\angle A = \angle APQ$ vì DE // PQ, nên $\angle AED = \angle APQ$. Tương tự, ta cũng có $\angle ADE = \angle AQP$. Do đó tam giác ADE và APQ đều có hai góc bằng nhau, tức là cân.
c) Ta có $\angle LBD = \angle LCB$ do cùng chắn cung LB trên đường tròn (T). Mà $\angle LCB = \angle LPB$ vì DE // PQ, nên $\angle LBD = \angle LPB$. Tương tự, ta cũng có $\angle LDC = \angle LQC$. Do đó tam giác LBD và LPQ đều có hai góc bằng nhau, tức là đồng dạng. Vậy ta có $\frac{LD}{LP} = \frac{LB}{LQ}$.
Từ đó, có $\frac{LP}{LQ} = \frac{LB}{LD}$. Áp dụng định lý cosin trong tam giác BPQ, ta có:
$PQ^2 = BP^2 + BQ^2 - 2BP \cdot BQ \cdot \cos{\angle PBQ}$
Nhưng ta cũng có:
$BP = LB \cdot \frac{LD}{LP}$
$BQ = L \cdot \frac{LP}{LD}$
Thay vào định lý cosin, ta được:
$PQ^2 = LB^2 + LQ^2 - 2LB \cdot LQ \cdot \frac{LD}{LP} \cdot \frac{LP}{LD} \cdot \cos{\angle PBQ}$
$PQ^2 = LB^2 + LQ^2 - 2LB \cdot LQ \cdot \cos{\angle PBQ}$
Tương tự, áp dụng định lý cosin trong tam giác ADE, ta có:
$DE^2 = AD^2 + AE^2 - 2AD \cdot AE \cdot \cos{\angle AED}$
Nhưng ta cũng có:
$AD = LD \cdot \frac{LB}{LP}$
$AE = LQ \cdot \frac{LD}{LP}$
Thay vào định lý cosin, ta được:
$DE^2 = LD^2 + LQ^2 - 2LD \cdot LQ \cdot \frac{LB}{LP} \cdot \frac{LD}{LP} \cdot \cos{\angle AED}$
$DE^2 = LD^2 + LQ^2 - 2LD \cdot LQ \cdot \cos{\angle AED}$
Nhưng ta cũng có $\angle AED = \angle PBQ$ do tam giác cân ADE và APQ, nên $\cos{\angle AED} = \cos{\angle PBQ}$. Do đó,
$DE^2 + PQ^2 = 2(LB^2 + LQ^2) - 4LB \cdot LQ \cdot \cos{\angle PBQ}$
Nhưng ta cũng có $LB \cdot LQ = LH \cdot LL'$ (với L' là điểm đối xứng của L qua AB), do tam giác HL'B cân tại L'. Thay vào phương trình trên, ta được:
$DE^2 + PQ^2 = 2(LB^2 + LQ^2) - 4LH \cdot LL' \cdot \cos{\angle PBQ}$

D M A J C O J B
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra : J là trung điểm của AB
Ta được : \(AJ=\frac{1}{2}AB=4cm\)
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 ( OA = R = 5cm )
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.
b) Kẻ OM vuông góc với CD tại M.
Tứ giác OJIM có :\(\widehat{I}=\widehat{J}=\widehat{M}=90^o\)nên là hcn
Ta có IJ = AJ – AI = 4 – 1 = 3cm
=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)
Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)

Lời giải chi tiết
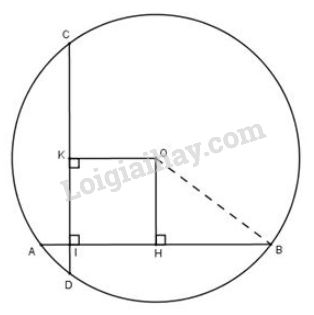
a) Kẻ OH⊥ABOH⊥AB tại H
Khi đó, đường tròn (O) có OH là 1 phần đường kính vuông góc với dây AB tại H
Suy ra HH là trung điểm của dây ABAB (Theo định lí 2 - trang 103)
⇒HA=HB=AB2=82=4cm.⇒HA=HB=AB2=82=4cm.
Xét tam giác HOBHOB vuông tại HH, theo định lí Pytago, ta có:
OB2=OH2+HB2⇔OH2=OB2−HB2OB2=OH2+HB2⇔OH2=OB2−HB2
⇔OH2=52−42=25−16=9⇒OH=3(cm)⇔OH2=52−42=25−16=9⇒OH=3(cm).
Vậy khoảng cách từ tâm OO đến dây ABAB là 3cm3cm.
b) Vẽ OK⊥CDOK⊥CD tại K
Tứ giác KOHIKOHI có ba góc vuông (ˆK=ˆH=ˆI=900)(K^=H^=I^=900) nên là hình chữ nhật, suy ra OK=HIOK=HI.
Ta có HI=AH−AI=4−1=3cmHI=AH−AI=4−1=3cm, suy ra OK=3cm.OK=3cm.
Vậy OH=OK=3cm.OH=OK=3cm.
Hai dây ABAB và CDCD cách đều tâm nên chúng bằng nhau.
Do đó AB=CD.
Lời giải chi tiết

a) Kẻ OH⊥ABOH⊥AB tại H
Khi đó, đường tròn (O) có OH là 1 phần đường kính vuông góc với dây AB tại H
Suy ra HH là trung điểm của dây ABAB (Theo định lí 2 - trang 103)
⇒HA=HB=AB2=82=4cm.⇒HA=HB=AB2=82=4cm.
Xét tam giác HOBHOB vuông tại HH, theo định lí Pytago, ta có:
OB2=OH2+HB2⇔OH2=OB2−HB2OB2=OH2+HB2⇔OH2=OB2−HB2
⇔OH2=52−42=25−16=9⇒OH=3(cm)⇔OH2=52−42=25−16=9⇒OH=3(cm).
Vậy khoảng cách từ tâm OO đến dây ABAB là 3cm3cm.
b) Vẽ OK⊥CDOK⊥CD tại K
Tứ giác KOHIKOHI có ba góc vuông (ˆK=ˆH=ˆI=900)(K^=H^=I^=900) nên là hình chữ nhật, suy ra OK=HIOK=HI.
Ta có HI=AH−AI=4−1=3cmHI=AH−AI=4−1=3cm, suy ra OK=3cm.OK=3cm.
Vậy OH=OK=3cm.OH=OK=3cm.
Hai dây ABAB và CDCD cách đều tâm nên chúng bằng nhau.
Do đó AB=CD.
* Mạng :))) *
#Ninh Nguyễn
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra: J là trung điểm của AB.
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 (OA = R = 5cm)
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.