Cho đường tròn (O), cung BC có số đo bằng 120 ° điểm A di chuyển trên cung lớn BC. Trên tia đối tia AB lấy điểm D sao cho AD = AC. Hỏi điểm D di chuyển trên đường nào?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 2 2018
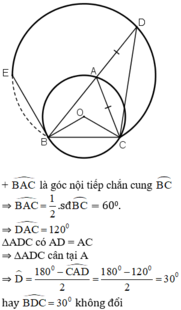
⇒ D nằm trên cung chứa góc 300 dựng trên đoạn BC.
+ Khi A ≡ C thì D ≡ C, khi A ≡ B thì D ≡ E (BE là tiếp tuyến của đường tròn (O) tại B).
Vậy khi A di chuyển trên cung lớn BC thì D di chuyển trên cung CE thuộc cung chứa góc 30º dựng trên BC.
25 tháng 4 2017
Hướng dẫn làm bài:
Giả sử, gọi cạnh hình vuông là a và bán kính đường tròn là R.
Khi đó, chu vi hình vuông là 4a và chu vi hình tròn là 2πR.
Theo đề bài ra ta có: 4a=2πR⇒a=πR24a=2πR⇒a=πR2
Ta lập tỉ số diện tích hình vuông và hình tròn:
ShvShtr=a2πR2=(πR22)πR2=π2R24πR2=π4<1ShvShtr=a2πR2=(πR22)πR2=π2R24πR2=π4<1 (vì π ≈ 3,14)
⇒ Shv < Shtr
Vậy hình tròn có diện tích lớn hơn hình vuông
25 tháng 4 2017
Hướng dẫn làm bài:
Ta có ˆA=12sđcungBC=600;ˆBDC=12.600=300A^=12sđcungBC=600;BDC^=12.600=300
Như vậy, điểm D tạo với hai mút của đoạn thẳng BC cố định một góc ˆBDC=300BDC^=300 nên D chuyển động trên cung chứa góc 30° dựng trên BC.
Ta có, khi A ≡ B thì D ≡ E và khi A ≡ C thì D ≡ C
Vậy khi A di chuyển trên cung lớn BC thì D di chuyển trên cung CE thuộc cung chưa góc 30° dựng trên BC
20 tháng 2 2020
Xét \(\Delta MBD\)cân tại M có :
\(\widehat{BDM}=60^0\)
\(\Rightarrow\Delta MBD\)là tam giác đều
\(\Rightarrow\widehat{BDM}=60^0\)
\(\Rightarrow\widehat{BDA}=120^0\)
\(\Rightarrow\)Khi M di chuyển trên cung nhỏ BC thì M di chuyển trên cung tròn ( nằm trên nửa mặt phẳng bờ AB chưa điểm M ) nhìn AB một góc bằng \(120^0\)
Xét \(\Delta DBA\)và \(\Delta MBC\)có :
\(BA=BC\)( vì tam giác ABC đều )
\(\widehat{BAD}=\widehat{BCM}\)( cùng chắn cung BM )
\(\widehat{ABD}=\widehat{CBM}\left(=60^0-\widehat{DBC}\right)\)
Suy ra \(\Delta DBA=\Delta MBC\)
\(\Rightarrow MC=DA\)
\(\Rightarrow MA+MB+MC=MA+MD+DA=2MA\)
\(MA+MB+MC\)lớn nhất khi MA lớn nhất
\(\Rightarrow AM\)là đường kính của \(\left(O\right)\)
\(\Rightarrow M\)là điểm chính giữa của cung BC
Chúc bạn học tốt !!!
⇒ D nằm trên cung chứa góc 30 ° dựng trên đoạn BC.
+ Khi A ≡ C thì D ≡ C, khi A ≡ B thì D ≡ E (BE là tiếp tuyến của đường tròn (O) tại B).
Vậy khi A di chuyển trên cung lớn BC thì D di chuyển trên cung CE thuộc cung chứa góc 30 ° dựng trên BC.