Cho lục giác đều ABCDEF.Chứng minh rằng đường chéo BF chia AD thành hai đoạn thẳng theo tỉ lệ 1 : 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
11 tháng 11 2018
Đúng(0)
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
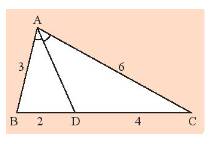
Ta có: \(\frac{{BD}}{{DC}} = \frac{2}{4} = \frac{1}{2};\frac{{AB}}{{AC}} = \frac{3}{6} = \frac{1}{2}\).
Do đó, đường phân giác \(AD\) của tam giác đã chia cạnh \(BC\) thành hai đoạn là \(BD\) và \(DC\) tỉ lệ với hai cạnh \(AB\) và \(AC\).
15 tháng 11 2015
Gọi BD là phân giác của HAC
=>tam giác ABD cân tại A( có AD dồng thời là dg cao và pgiac)
=> BH=DH = 3a => DC =5a vì BH:HC =3:8
+ Áp dụng tính chất đường phân giác trong tam giác HAC
ta có : AC/AH =DC/DH
=> AC/6 =5/3 => AC =10
+ Áp dụng pita go cho HAC => HC = 8 => a =1
=>BC = 11a =11
=>S =AH.BC/2 =6.11/2 =33
29 tháng 8 2015
Dễ ẹt;
C A B Chữ kí của tui D I H
Giả sử \(\Delta\)ABC vuông tại A có phân giác AD sao cho DC=3BD;đương cao AH
Từ B kẻ đường thẳng song song với AC cắt AD tại I => BI vuông góc AB
Vì AD là p/g góc A => góc BAD=45 nên tam giác BAI vuông cân tại B nên BA=BI
Vì BI // AC nên \(\left(\frac{BI}{AC}\right)=\left(\frac{BD}{DC}\right)=\left(\frac{BD}{3BD}\right)=\frac{1}{3}\) (định lí Ta lét)
mà BI=AB nên \(\frac{AB}{AC}=\frac{1}{3}\)
Cm \(\Delta\)AHC đồng dạng \(\Delta\)BHA(g.g) nên \(\frac{BH}{HA}=\frac{HA}{HC}=\frac{AB}{AC}=\frac{1}{3}\)
nên \(BH=\frac{1}{3}AH\);\(HC=3AH\)nên \(\frac{BH}{HC}=\frac{1}{9}\)
6 tháng 9 2024
Giả sử
Δ
ΔABC vuông tại A có phân giác AD sao cho DC=3BD;đương cao AH
Từ B kẻ đường thẳng song song với AC cắt AD tại I => BI vuông góc AB
Vì AD là p/g góc A => góc BAD=45 nên tam giác BAI vuông cân tại B nên BA=BI
Vì BI // AC nên
(
B
I
A
C
)
=
(
B
D
D
C
)
=
(
B
D
3
B
D
)
=
1
3
(
AC
BI
)=(
DC
BD
)=(
3BD
BD
)=
3
1
(định lí Ta lét)
mà BI=AB nên
A
B
A
C
=
1
3
AC
AB
=
3
1
Cm
Δ
ΔAHC đồng dạng
Δ
ΔBHA(g.g) nên
B
H
H
A
=
H
A
H
C
=
A
B
A
C
=
1
3
HA
BH
=
HC
HA
=
AC
AB
=
3
1
nên
B
H
=
1
3
A
H
BH=
3
1
AH;
H
C
=
3
A
H
HC=3AHnên
B
H
H
C
=
1
9
HC
BH
=
9
1
GN
25 tháng 2 2018
dễ dàng chứng minh được EBFD là hình bình hành => FB // DE
gọi I là giao điểm của DE và AC ; K là giao điểm của FB và AC
ta có: FB là đường trung bình của tam giác DIC => FB chia IC thành hai đoạn bằng nhau (1)
tương tự chứng minh được DE là đường trung bình của tam giác AKB => DE chia AK thành hai đoạn bằng nhau (2)
Từ 1 và 2 => đpcm
*Bên trên là gợi ý thôi bạn tự trình bày nhé =))))
5 tháng 3 2020
A B C D E F T G
íu biết thì cut hộ
Gọi T,G là giao điểm DE,BF với AC
Ta có:AB=CD nên \(\frac{1}{2}AB=\frac{1}{2}CD\Rightarrow EB=DF\) mà \(EB//DF\) nên tứ giác EBFD là hình bình hành => ED//BF
Xét \(\Delta\)ABG có EA=EB;ET//BG nên T là trung điểm AG hay TA=TG ( 1 )
Xét \(\Delta\)CDT có FD=FC;FG//DT nên G là trung điểm CT hay TG=GC ( 2 )
Từ ( 1 ) và ( 2 ) suy ra đpcm