Giải các phương trình : 3,4 x 2 + 8,2x = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 5 2022
a: =>x(7x-5)=0
=>x=0 hoặc x=5/7
b: \(\Leftrightarrow\sqrt{2}x^2-6x=0\)
\(\Leftrightarrow x\left(\sqrt{2}x-6\right)=0\)
hay \(x\in\left\{0;3\sqrt{2}\right\}\)
c: =>x(3,4x+8,2)=0
=>x=0 hoặc x=-82/34=-41/17
d: \(\Leftrightarrow x\left(\dfrac{2}{5}x+\dfrac{7}{3}\right)=0\)
=>x=0 hoặc x=-35/6
HM
1
R
20 tháng 1 2021
a) \(2x-10=0\)
\(\Leftrightarrow2x=10\)
\(\Leftrightarrow x=5\)
Vậy tập nghiệm của phương trình là: S = {5}
b) \(3,4-x=-4\)
\(\Leftrightarrow x=7,4\)
Vậy tập nghiệm của phương trình là: S = {7,4}
c) \(x-\frac{4}{5}=\frac{1}{5}\)
\(\Leftrightarrow x=1\)
Vậy tập nghiệm của phương trình là: S = {1}
d) \(2\left(x-3\right)-3x+5=0\)
\(\Leftrightarrow2x-6-3x+5=0\)
\(\Leftrightarrow-x-1=0\)
\(\Leftrightarrow x=-1\)
Vậy tập nghiệm của phương trình là: S = {-1}
21 tháng 1 2021
a, \(2x-10=0\Leftrightarrow x=5\)
Vậy tập nghiệm của phương trình là S = {5}
b, \(3,4-x=-4\Leftrightarrow x=7,4\)kết luận tương tự như trên và các phần còn lại
c, \(\frac{x-4}{5}=\frac{1}{5}\)Khử mẫu : \(x-4=1\Leftrightarrow x=5\)
d, \(x+12=2-x\Leftrightarrow2x=-10\Leftrightarrow x=-5\)
e, \(2\left(x-3\right)-3x+5=0\Leftrightarrow2x-6-3x+5=0\)
\(\Leftrightarrow-x-1=0\Leftrightarrow x=-1\)
24 tháng 2 2021
`a,(x+3)(x^2+2021)=0`
`x^2+2021>=2021>0`
`=>x+3=0`
`=>x=-3`
`2,x(x-3)+3(x-3)=0`
`=>(x-3)(x+3)=0`
`=>x=+-3`
`b,x^2-9+(x+3)(3-2x)=0`
`=>(x-3)(x+3)+(x+3)(3-2x)=0`
`=>(x+3)(-x)=0`
`=>` $\left[ \begin{array}{l}x=0\\x=-3\end{array} \right.$
`d,3x^2+3x=0`
`=>3x(x+1)=0`
`=>` $\left[ \begin{array}{l}x=0\\x=-1\end{array} \right.$
`e,x^2-4x+4=4`
`=>x^2-4x=0`
`=>x(x-4)=0`
`=>` $\left[ \begin{array}{l}x=0\\x=4\end{array} \right.$
24 tháng 2 2021
1) a) \(\left(x+3\right).\left(x^2+2021\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\x^2+2021=0\end{matrix}\right.\\\left[{}\begin{matrix}x=-3\left(nhận\right)\\x^2=-2021\left(loại\right)\end{matrix}\right. \)
=> S={-3}
27 tháng 3 2018
3.4x^2+8.2x=0
<=>x(3.4x+8.2)=0
<=>x=0 hoặc 3.4x+8.2=0
<=>x=0 hoặc x=-8.2/3.4=-41/17
27 tháng 3 2018
3,4x2 + 8,2x = 0
<=> x(3,4x + 8,2) = 0
<=> \(\hept{\begin{cases}x=0\\3,4x+8,2=0\end{cases}\hept{\begin{cases}x=0\\x\approx2,41\end{cases}}}\)
; 
;2x2 + 3 = 0 ; 4– 0,2x = 0
QN
20 tháng 3 2022
a) PT bậc nhất một ẩn là: x-2=0; 4-0,2x=0
b) Giải:
x-2=0 (*)
⟺ x=-2
Vậy tập nghiệm của pt (*) là S={-2}
4-0,2x=0 (**)
⟺-0,2x=-4
⟺x=-4/-0,2=20
Vậy tập nghiệm của pt (**) là S={20}
AH
Akai Haruma
Giáo viên
6 tháng 1 2023
Bài 9:
Không, vì $x+2=0$ có nghiệm duy nhất $x=-2$ còn $\frac{x}{x+2}=0$ ngay từ đầu đkxđ đã là $x\neq -2$ (cả 2 pt không có cùng tập nghiệm)
AH
Akai Haruma
Giáo viên
6 tháng 1 2023
Bài 8:
a. Khi $m=2$ thì pt trở thành:
$(2^2-9)x-3=2$
$\Leftrightarrow -5x-3=2$
$\Leftrightarrow -5x=5$
$\Leftrightarrow x=-1$
b.
Khi $m=3$ thì pt trở thành:
$(3^2-9)x-3=3$
$\Leftrightarrow 0x-3=3$
$\Leftrightarrow 0=6$ (vô lý)
c. Khi $m=3$ thì pt trở thành:
$[(-3)^2-9]x-3=-3$
$\Leftrightarrow 0x-3=-3$ (luôn đúng với mọi $x\in\mathbb{R}$)
Vậy pt vô số nghiệm thực.
CM
18 tháng 9 2017
(x - 2 ) + 3( x 2 – 2) = 0 ⇔ (x - 2 )+ 3(x + 2 )(x - 2 ) = 0
⇔ (x - 2 )[1 + 3(x + 2 )] = 0 ⇔ (x - 2 )(1 + 3x + 3 2 ) = 0
⇔ x - 2 = 0 hoặc 1 + 3x + 3 2 = 0
x - 2 = 0 ⇔ x = 2
1 + 3x + 3
2
= 0 ⇔ x =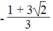 
Vậy phương trình có nghiệm x =
2
hoặc x =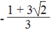 
Ta có: 3,4 x 2 + 8,2x = 0 ⇔ x(3,4x + 8,2) = 0
⇔ x = 0 hoặc 3,4x + 8,2 = 0 ⇔ x = 0 hoặc x = -(8,2)/(3,4)
Vậy phương trình có hai nghiệm: x 1 = 0, x 1 = -(4,1)/(1,7)