Cho hình 36. Hãy viết hệ thức giữa:
Các cạnh góc vuông p, r và đường cao h.
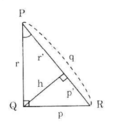
Hình 36
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
25 tháng 9 2019
Đúng(0)
Những câu hỏi liên quan
14 tháng 12 2021
\(a,AH^2=BH.BC\)
\(b,\)Áp dụng hệ thức lượng vào \(\Delta ABC\) vuông tại \(A\),đường cao \(AH\) có:
\(AH^2=BH.BC\)
\(\Rightarrow AH^2=4.9\)
\(\Rightarrow AH^2=36\Rightarrow AH=6\left(cm\right)\)
4 tháng 12 2018
A B C H 4cm 9cm
A. Hệ thức liên hệ giữa đường cao và hình chiếu của các cạnh góc vuông trên cạnh huyền: \(AH^2=BH.CH\)
B. Ta có △ABC vuông tại A có đường cao AH\(\Rightarrow AH^2=BH.CH=4.9=36\Rightarrow AH=6\left(cm\right)\)
MT
1 tháng 4 2017
Hạ đường sinh AA1 vuông góc với đáy chứa cạnh CD. Khi đó góc ADA1 là góc giữa hai mặt phẳng hình vuông và mặt đáy.
Vì góc A1DC = 1v nên A1C là đường kính.
Gọi cạnh hình vuông là a.
Ta có
a2 = AD2 = AA12 + A1D2
mà AA1 = h = r, nên ta có:
A1D2 + DC2 = A1C2;
a2 – r2 + a2 = 4r2;
⇒a2=52r2
Vậy diện tích hình vuông là: SABC=a2=52r2
Gọi δ = góc ADA1 là góc tạo bởi mặt phẳng hình vuông và đáy, ta có:
sinδ = A1AAD=ra=√25