Cho đoạn thẳng CD
Chứng minh rằng các điểm N1, N2, N3 nằm trên đường tròn đường kính CD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 3 2018
Vẽ Hình
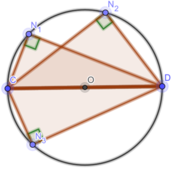
b) Vì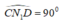 
nên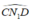 
là góc nội tiếp chắn nửa đường tròn đường kính CD hay
N
1
,
nằm trên đường tròn đường kính CD
Tương tự như vậy ta chứng minh được N 2 , N 3 nằm trên đường tròn đường kính CD
Vậy N 1 , N 2 , N 3 nằm trên đường tròn đường kính CD
AT
13 tháng 8 2016
Nhận thấy tứ giác MFNE có góc M và N vuông --> góc MFN+góc MEN= 2 vuông (*)
Lại có các tam giác AFB và MEN đồng dạng (vì có góc NME=gocFAB và góc MNE =góc FBA), suy ra góc AFB=góc MEN --> góc MFN=góc MEN (**), từ (*); (**) suy ra góc MFN=góc MEN =1 vuông
--> tứ giác MENF là hình chữ nhật, từ đó dễ dàng suy ra tiếp FE vuông góc với AB
b) Gọi I ; K lần lượt là trung điểm của O1O2 và MN. Áp dụng Talét dễ dàng tính được IK=5
--> KD^2=ID^2-IK^2 =9^2 -5^2 =56 --> CD=2.KD= 4√14
PT
1
PT
1
PT
1
10 tháng 12 2023
a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>OBAC là tứ giác nội tiếp đường tròn đường kính OA
=>O,B,A,C cùng thuộc đường tròn đường kính OA
Tâm của đường tròn là trung điểm của OA
b: Xét (O) có
AB,AC là tiếp tuyến
DO đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC
Xét (O) có
ΔBCD nội tiếp
CD là đường kính
Do đó: ΔCBD vuông tại B
=>CB\(\perp\)BD
Ta có: CB\(\perp\)BD
BC\(\perp\)OA
Do đó: OA//BD
Vì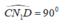
nên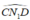 
là góc nội tiếp chắn nửa đường tròn đường kính CD hay N1 nằm trên đường tròn đường kính CD
Tương tự như vậy ta chứng minh được N2,N3 nằm trên đường tròn đường kính CD
Vậy N1,N2,N3 nằm trên đường tròn đường kính CD