cho tam giác abc nhọn.gọi d là trung điểm của ab.lấy e đối xứng với c qua điểm d
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sửa đề: EF//AB(F thuộc BC)
Xét tứ giác AKCF có
E là trung điểm chung của AC và KF
=>AKCF là hbh
=>AK//CF
=>AK//BC

Xét tam giác COA tao có FD là đường trung bình
=> FD = 1/2 A'C'
chứng minh tương tự FD = 1/2 AC => A'C' =AC
chứng minh tương tự B'C"= BC; A'B'=AB
vậy tam giác ABC =tam giác A'B'C'

A B C M N D E
Xét \(\Delta DAM\) và \(\Delta CBM\) có:
\(BM=AM\left(gt\right);\widehat{DMA}=\widehat{CMB}\left(đ.đ\right);DM=MC\left(đ.đ\right)\Rightarrow\Delta DAM=\Delta CBM\left(c.g.c\right)\)
\(\Rightarrow\widehat{DAM}=\widehat{CBM}\) ( 1 )
Tương tự \(\Delta AEN=\Delta CBN\left(c.g.c\right)\Rightarrow\widehat{EAN}=\widehat{BCN}\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra:\(\widehat{DAM}+\widehat{EAN}=\widehat{CBM}+\widehat{BCN}\)
\(\Rightarrow\widehat{DAM}+\widehat{EAN}+\widehat{BAC}=\widehat{CBM}+\widehat{BCN}+\widehat{BAC}\Rightarrow\widehat{DAE}=180^0\)
=> D,A,E thẳng hàng.
Mặt khác \(DA=BC;EA=BC\Rightarrow DA+EA=2BC\Rightarrow DE=2BC\Rightarrow DA=EA\Rightarrowđpcm\)

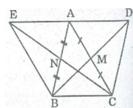
* Xét tứ giác ABCD, ta có:
MA = MC (gt)
MB = MD (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ AD // BC và AD = BC (1)
* Xét tứ giác ACBE, ta có:
AN = NB (gt)
NC = NE (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ACBE là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường) ⇒ AE // BC và AE = BC (2)
Từ (1) và (2) suy ra: A, D, E thẳng hàng và AD = AE
Nên A là trung điểm của DE hay điểm D đối xứng với điểm E qua điểm A.
xét tam giác ADE có:
AB=DB( gt)
AC=EC (gt)
=> BC//DE ( t/c đường trung bình)
ta có: BC//DE (CMT)
AM vuông góc với BC
AM=IM
=> góc AID= góc AIE
Xét tam giác AEI và tam giác ADIcó:
góc DAI= góc EAI
AI chung
góc AID= góc AIE (CMT)
=> tam giác AEI = tam giác ADI (g.c.g)
=> DI=EI(2 cạnh tương ứng)

a: Xét tứ giác AEBM có
D là trung điểm của AB
D là trung điểm của EM
Do đó: AEBM là hình bình hành

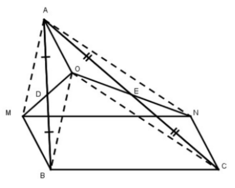
* Xét tứ giác AOBM, ta có:
DA = DB (gt)
DO = DM (định nghĩa đối xứng tâm)
Suy ra: Tứ giác AOBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ BM // AO và BM = AO (1)
* Xét tứ giác AOCN, ta có: EA = EC (gt)
EO = EN (định nghĩa đối xứng tâm)
Suy ra: Tứ giác AOCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ CN // AO và CN = AO (2)
Từ (1) và (2) suy ra:BM // CN và BM = CN.
Vậy tứ giác BMNC là hình bình hành (vì có 1 cặp cạnh đối song song và bằng nhau).
Đề bài yêu cầu gì?