Cho đồ thị vận tốc – thời gian của một xe chuyển động trên đường thẳng. Gia tốc của xe trong khoảng thời gian (5 -> 10s ) là:
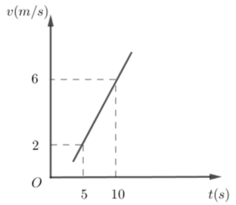
A. 0,2m/ s 2
B. 0,4m/ s 2
C. 0,6m/ s 2
D. 0,8m/ s 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 9 2016
chọn hệ quy chiếu: gốc tọa độ trùng A
chiều dượng của Ox từ A đến B
gốc thời gian khi ô tô đi qua điểm A ( lúc 8h)
a) phương trình chuyển động của 2 xe
x1=10t - 0,1t^2
x2= 560 - 0,2t^2
2 xe gặp nhau <=> x1=x2
<=> t=40s
x=x1=x2= 240m
b) phương trình vận tốc của 2 xe: (v=v0 + at)
v1=10 - 0,2 .40 =2 m/s
v2= 0+ 0,4 .40 = 16 m/s
3 tháng 9 2016
Chọn gốc thời gian là lúc 8h, gốc tọa độ tại A, chiều dương từ A đến B
ô tô 1: xo1 = 0; vo1 = 10m/s; a1 = -0,2m/s2
ô tô 2: xo1 = 560; vo1 = 0; a1 = 0,4m/s2
Giải
a) Phương trình chuyển động của hai xe:
x1 = x01 + v01t + 0,5a1t2 = 10t – 0,1t2 (1)
x2 = x02 + v02t + 0,5a2t2 = 560 – 0,2t2 (2)
b) Khi hai xe gặp nhau:
x1 = x2 => 10t – 0,1t2 = 560 – 0,2t2 => t = 40 s
=> x1 = x2 = 240 m.
c) Thời gian để xe một dừng lại:
v1 = vo1 + a1.t => t = 50 s;
LN
11 tháng 8 2016
a,ta có gốc A chiều + AB => X1=Xo+Vot+1/2at^2 vs Xo=0; Vo=10 ;a=-0.2(chậm dần)
=>X1=10t-0.1t^2
xe2 ở B có Xo=560 ,Vo=0 ,a=0.4 => X2=560-0.2t^2 ( xe 2 đi ngược lại B>A )
b,2 xe gặp nhau khi X1=X2 <=> 10t-0.1t^2=560-0.2t^2 <=> t=40(n) t=-140(l)
S1=Vot+1/2at^2=10*40 -0.1*40^2=240
S2=Vot+1/2at^2=0.2*40^2=320
c,tại thời điểm 2 xe gặp nhau t=40 => v xe1 lúc gặp nhau ;V1=Vo-at=10-0.2*40=2
V2=Vo +at=0.4*40=16
vẽ trục oy là v; ox là t trên oy lấy các điểm 2,10,16 trên ox lấy điểm 40 . vẽ đt x1 từ 10 đến giao điểm của 2 vs 40 . vẽ x2 từ 0 đến giao 16 vs 40
VT
21 tháng 3 2017
+ Trong khoảng thời gian từ 0 đến t 1 thuộc chuyển động nhanh dần đều (vì vận tốc tăng)
+ Trong khoảng thời gian từ t 1 đến t 2 thuộc chuyển động thẳng đều (vì vận tốc không đổi)
+ Trong khoảng thời gian từ t 2 đến t 3 thuộc chuyển động chậm dần đều (vì vận tốc giảm) => Chọn C
VT
13 tháng 9 2017
Chọn C.
Trong chuyển động thẳng chậm dần đều, đồ thị vận tốc thời gian là đường thẳng chéo xuống (v giảm đều theo t).
12 tháng 9 2018
chọn gốc tọa độ tại điểm A, chiều dương từ A-B, gốc thời gian lúc 8h
a)x1=x0+v.t+a.t2.0,5=t-0,1t2
x2=x0+v.t+a.t2.0,5=560-0,2t2
hai xe gặp nhau \(\Rightarrow\)x1=x2\(\Rightarrow\)t=70s
vậy hai xe gặp nhau sau 70s
b) hai xe gặp nhau lúc 8h 70s
c) hai xe gặp nhau lúc 8h 70s
19 tháng 7 2018
Bài 1
Chọn trục Ox trùng với quỹ đạo chuyển động , gốc tọa độ O ở A , chiều dương là chiều chuyển động của xe ô tô . Mốc thời gian t0=0 lúc 7h
a)
Với xe ô tô ở A \(\left\{{}\begin{matrix}ở.t0=0.có.v01=5\left(\dfrac{m}{s}\right)\\ở.t1=10s.có.v1=10\left(\dfrac{m}{s}\right)\end{matrix}\right.\) có x01 =0 ( do A trùng O)
=> a = \(\dfrac{v1-v01}{t1-t0}=\dfrac{10-5}{10-0}=0,5\left(\dfrac{m}{s^2}\right)\)
=> PTCĐ : x1= x01 + v0(t-t0) + 1/2.a.(t-t0)^2 <=> x1= 0 + 5(t-0)+1/2.0,5.(t-0)^2
<=> x1 = 5t + 0,25.t^2(t\(\ge0\))
Với xe máy ở B lúc t0 = 0 có v = 36km/h=10m/s , x02 = 100m
=> PtCĐ : x2 = x02 + v2(t-t0) <=> x2 = 100 + 10t (t\(\ge0\))
b) 2 xe gặp nhau thì
x1 = x2
<=> 5t + 0,25t^2 = 100+10t <=> 0,25t^2 -5t-100=0(t\(\ge0\))
=> \(\left\{{}\begin{matrix}t\approx32,36\left(s\right)\left(nhận\right)\\t\approx-12,36\left(s\right)\left(loại\right)\end{matrix}\right.\)
thay t = 32,36 vào x2(x1=x2) ta được : x1 = 100+10.t = 100 + 10.32,36 = 432,6(m)
Vậy 2 xe gặp nhau sau 32,36 giây và cách A 432,6 m
19 tháng 7 2018
bài 2 tương tự thôi , bạn tự làm nha , câu b có hơi khác , bạn muốn tính v mỗi xe thì thay t lúc gặp nhau vào công thức tính vận tốc v = v0 + at , quãng đường thì cũng tương tự như thế , thay t, v0 của mỗi xe , a của mỗi xe vào công thức s = v0.t+1/2a.t^2 là ra :v
Đáp án D