Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D.
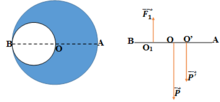
Sử dụng quy hợp lực song song ngược chiều. Ta được:
( ở đây ta coi F1 giống như một lực nâng có độ lớn bằng trọng lượng phần khoét đi lên biểu thị cho phần lỗ tròn rỗng, và P là trọng lực của cả đĩa tròn khi chưa khoét)
Đĩa tròn đồng chất
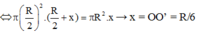
Chọn D.
Gọi P → là trọng lượng của đĩa bán kính R khi chưa bị khoét, P 1 → là trọng lượng của đĩa nhỏ có bán kính R/2 và P 2 → là trọng lượng của phần đĩa còn lại sau hai lần khoét, ta có:
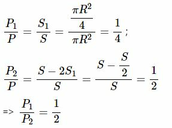
Do tính chất đối xứng, trọng tâm phần đĩa còn lại sau hai lần khoét thì trùng với tâm O của đĩa khi chưa khoét, còn trọng tâm của đĩa nhỏ mà ta giả sử khoét thêm thì ở tâm O 1 của nó. Gọi G là trọng tâm của đĩa sau khi bị khoét một lỗ tròn. Ta có hệ phương trình
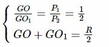
Giải ra ta được:
Chọn D
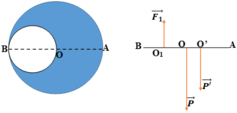
Sử dụng quy hợp lực song song ngược chiều. Ta được:
F 1 . O 1 O' = P.OO' (ở đây ta coi F 1 giống như một lực nâng có độ lớn bằng trọng lượng phần khoét đi lên biểu thị cho phần lỗ tròn rỗng, và P là trọng lực của cả đĩa tròn khi chưa khoét)
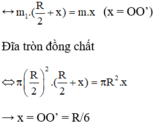
+)Gọi OH là bán kính của đường tròn nhỏ => OH vuông góc với AB
Ta có: OA = 1/2 AC
mà AC = \(a\sqrt{2}\)
=> OA = 1/2 . \(a\sqrt{2}=\frac{a\sqrt{2}}{2}\)
HA = 1/2 AB = 1/2 a = a/2
Trong tam giác vuông AOH có:
\(OH=\sqrt{AO^2-AH^2}=\sqrt{\left(\frac{a\sqrt{2}}{2}\right)^2-\left(\frac{a}{2}\right)^2}=\frac{a}{2}\)
Vậy bán kính đường tròn nhỏ = a/2
+) Bán kính đường tròn lớn = AO = \(\frac{a\sqrt{2}}{2}\)
Đáp án D
Sử dụng quy hợp lực song song ngược chiều. Ta được: F 1 . O 1 O ' = P . O O ' (ở đây ta coi F1 giống như một lực nâng có độ lớn bằng trọng lượng phần khoét đi lên biểu thị cho phần lỗ tròn rỗng, và P là trọng lực của cả đĩa tròn khi chưa khoét)