Do không thể đo trực tiếp bề rộng của một hòn đảo, nguời ta xây dựng mô hình như hình vẽ bên. Biết rằng E,F lần lượt là trung điểm của AB, AC. Biết EF=12km, khoảng cách từ B đến C của hòn đảo là
24 km
24 m
6 km
12 m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định li Py - ta - go vào △ ABC vuông tại C ta có:
AB2 = BC2 + AC2
AB2 = 122 + 52 = 169
⇒ AB = \(\sqrt{169}=13\)
Vậy cáp treo được xây dựng dài 13 km

Đáp án B.
Ta gọi A D = x 0 ≤ x ≤ 50 (km)
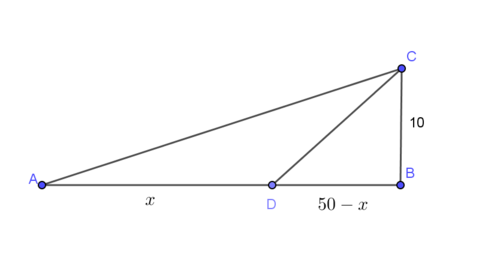
Khi đó: B D = 50 − x ; C D = 100 + 50 − x 2
Từ đó chi phí đi lại là:
f x = 3. x + 5. 100 + 50 − x 2 = 3 x + 5 x 2 − 100 x + 2600
Ta cần tìm để chi phí này là thấp nhất.
Ta có: f ' x = 3 + 5 2 x − 100 2 x 2 − 100 x + 2600 ;
f ' x = 0 ⇔ 6 x 2 − 100 x + 2600 = 500 − 10 x
⇔ x = 42 , 5.
Ta có: f 0 , f 2 < f 42 , 5
Vậy A D = 42 , 5 = 85 2 thì chi phí đi lại là thấp nhất.

Đáp án B
Đặt A D = x ⇒ B D = A B − A D = 40 − x ⇒ C D = B D 2 + B C 2 = 40 − x + 10 2
Suy ra kinh phí người đó phải bỏ là T = 3 x + 5 x 2 − 80 x + 1700 → f x
Khảo sát hàm số f(x)trên (0;40) suy ra min f x = 160 ⇔ x = 65 2 k m
Và chi phí người đó chỉ đi đường thủy là t = 5 40 2 + 10 2 = 500 17 U S D
VẬY kinh phí nhỏ nhất cần bỏ ra khi đi đường bộ là 65/2

Đáp án B
Gọi x (km) là quãng đường bộ mà người đó đi, 0 ≤ x ≤ 50
Suy ra, người đó phải đi với quãng đường thủy là



BC=2EF=24km
24km