Xét góc lượng giác (OA; OM) = α, trong đó M là điểm không làm trên các trục tọa độ Ox và Oy. Khi đó M thuộc góc phần tư nào để sinα và cosα cùng dấu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

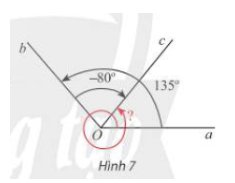
a, Số đo của góc lượng giác (Oa, Ob) trong Hình 7 là \(135^o+n\cdot360^o,n\in Z\)
Số đo của góc lượng giác (Oa, Ob) trong Hình 7 là \(-80^o+m\cdot360^o,m\in Z\)
Số đo của góc lượng giác (Oa, Ob) trong Hình 7 là \(415^o+k\cdot360^o,k\in Z\)
b, \(\left(Oa,Ob\right)+\left(Ob,Oc\right)=135^o+n\cdot360^o+\left(-80^o\right)+m\cdot360^o\\ =55^o+\left(n+m\right)\cdot360^o\\ =415^o+\left(n+m-1\right)\cdot360^o\\ =415^o+k\cdot360^o=\left(Oa,Oc\right)\)
Với \(k=n+m-1;n,m,k\in Z\)

a) Hoành độ của điểm M và M’ bằng nhau
Tung độ của điểm M và M’ đối nhau
b) Mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha \,\,v\`a \,\, - \alpha \)


Tham khảo:
a) 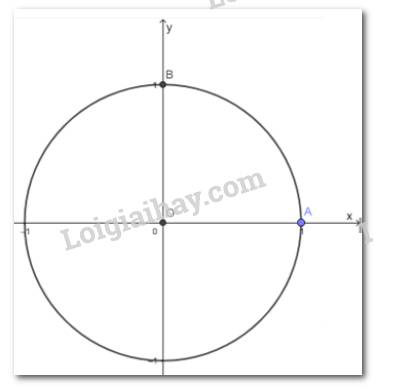
Góc lượng giác \(\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}\)
b)
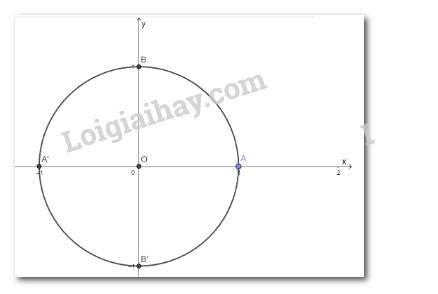

\(\begin{array}{l}\cos \left( { - 30^\circ } \right) = \frac{{\sqrt 3 }}{2} > 0\\\sin \left( { - 30^\circ } \right) = - \frac{1}{2} < 0\\\tan \left( { - 30^\circ } \right) = - \frac{{\sqrt 3 }}{3} < 0\\\cot \left( { - 30^\circ } \right) = - \sqrt 3 < 0\end{array}\)

Do \(\frac{\pi }{2} < \frac{{5\pi }}{6} < \pi \) nên
\(\begin{array}{l}\cos \left( {\frac{{5\pi }}{6}} \right) < 0\\\sin \left( {\frac{{5\pi }}{6}} \right) > 0\\\tan \left( {\frac{{5\pi }}{6}} \right) < 0\\\cot \left( {\frac{{5\pi }}{6}} \right) < 0\end{array}\)

Xét ΔABC vuông tại A có
\(sinB=\dfrac{AC}{BC}\)
\(cosB=\dfrac{AB}{BC}\)
\(tanB=\dfrac{AC}{AB}\)
\(cotB=\dfrac{AB}{AC}\)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}\)
\(cosC=\dfrac{AC}{BC}\)
\(tanC=\dfrac{AB}{AC}\)
\(cotC=\dfrac{AC}{AB}\)
Nhận xét:
\(sinB=cosC\)
\(sinC=cosB\)
\(tanB=cotC\)
\(cotB=tanC\)

Tham khảo:
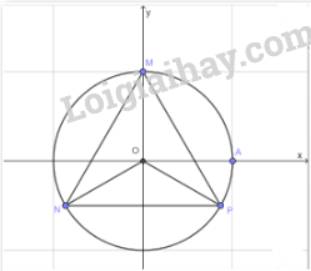
\(\begin{array}{l}(OM,ON) = (OA,ON) - (OA,OM) = \frac{{2\pi }}{3}\\ \Rightarrow \widehat {MON} = {120^0}\\\widehat {MOP} = \widehat {MOA} + \widehat {AOP} = {90^0} + {30^0} = {120^0}\\ \Rightarrow \widehat {NOP} = {360^0} - {120^0} - {120^0} = {120^0}\end{array}\)
Cung MP = cung NP = cung NM
\(\Rightarrow MP = NP = NM\)
\(\Rightarrow \Delta MNP\) đều

x O y A B C
Ta nối O với A.
Xét \(\Delta OAB\) và \(\Delta OAC\) có :
\(\hept{\begin{cases}\widehat{OBA}=\widehat{OCA=90^o}\\OAchung\\OB=OC\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta OAB=\Delta OAC\) ( cạnh huyền - cạnh góc vuông )
\(\Rightarrow\widehat{BOA}=\widehat{COA}\)
\(\Rightarrow OA\) là tia phân giác của \(\widehat{xOy}\)
*) Nhận xét : Tập hợp các điểm cách đều hai cạnh của một góc thì nằm trên tia phân giác của góc đó.

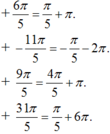
Chọn B.
Dựa theo định nghĩa các giá trị lượng giác trên đường tròn lượng giác.
Khi M nằm trong góc phần tư thứ nhất thì sin α và cosα cùng dương hoặc khi M nằm trong góc phần tư thứ ba thì sinα và cosα cùng âm.