Tìm m để các hàm số f ( x ) = x + 1 - 1 x k h i x > 0 2 x 2 + 3 m + 1 k h i x ≤ 0 liên tục trên R.
A. 1
B. -1/6
C. 2
D. 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có \(f\left(x\right)>0,\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-x^2-2\left(m-1\right)x+2m-1>0,\forall x\left(0;1\right)\)
\(\Leftrightarrow-2m\left(x-1\right)>x^2-2x+1,\forall x\in\left(0;1\right)\) (*)
Vì \(x\in\left(0;1\right)\Rightarrow x-1< 0\) nên (*) \(\Leftrightarrow-2m< \dfrac{x^2-2x+1}{x-1}=x-1=g\left(x\right),\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-2m\le g\left(0\right)=-1\Leftrightarrow m\ge\dfrac{1}{2}\)
a) * f(-2)
=-2.(-2)+1
=2
* f(3)
=-2.3+1
=-5
b) hàm số y=-2x+1
với x=-1 thì y=3 không bằng 1
Vậy M(-1,1)ko thuộc đồ thị hàm số f(x)
c) ta có 1>0
=> -2x+1=1
-2x=1-1
-2x=0
x=0/(-2)
x=0
=> x=0
vậy x=0 thì f(x)>0
nhớ k giùm mình nha
a)\(F\left(-2\right)=-2.\left(-2\right)+1=5\)
\(F\left(\frac{1}{2}\right)=-2.\left(\frac{1}{2}\right)+1=0\)
\(F\left(3\right)=-2.3+1=-5\)
\(F\left(1\right)=-2.1+1=-1\)
`f'(x) = x^2 - 4x+m`
`f'(x) >=0 <=>x^2-4x+m>=0`
`<=> \Delta' >=0`
`<=> 2^2-1.m>=0`
`<=> m<=4`
Vậy....
Câu 5:
a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)
\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)
\(f\left(0\right)=7\cdot0-3=-3\)
b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:
\(2\left(2m+1\right)-3=3\)
=>2(2m+1)=6
=>2m+1=3
=>2m=2
=>m=1
c: Thay m=1 vào hàm số, ta được:
\(y=\left(2\cdot1+1\right)x-3=3x-3\)
*Vẽ đồ thị
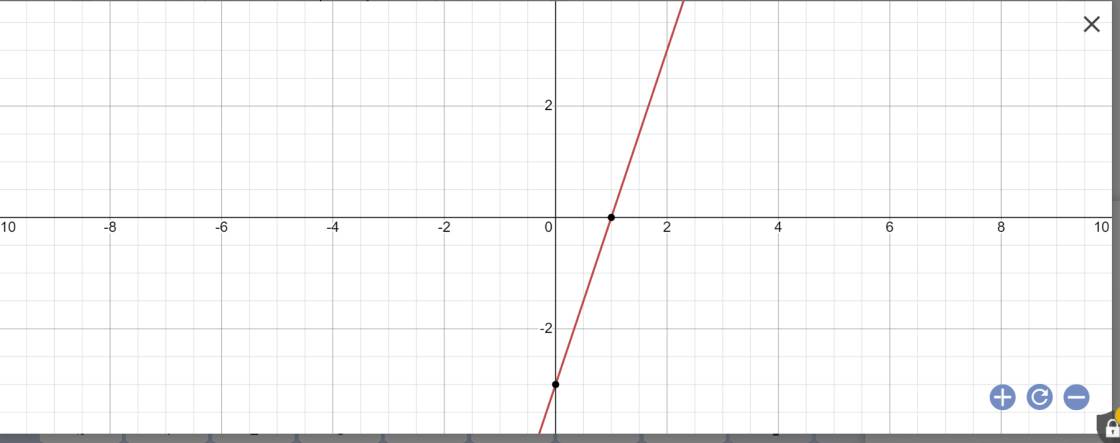
d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)
=>\(2m\ne-1\)
=>\(m\ne-\dfrac{1}{2}\)
e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)
=>2m+1=5
=>2m=4
=>m=2
Chọn B.
- Với x > 0 ta có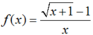
nên hàm số liên tục trên (0; +∞)
- Với x < 0 ta có f(x) = 2x2 + 3m + 1 nên hàm số liên tục trên (-∞; 0).
Do đó hàm số liên tục trên R khi và chỉ khi hàm số liên tục tại x = 0
Ta có: f(0) = 3m + 1
Do đó hàm số liên tục tại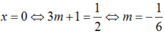
.