Cho các số thực dương x, y thỏa mãn: x + y = 5 4 thì biểu thức S = 4 x + 1 4 y đạt giá trị nhỏ nhất khi x = a y = b thì a.b có giá trị là bao nhiêu?
A. a . b = 3 8
B. a . b = 25 64
C. a . b = 0
D. a . b = 1 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Từ x + y = 5 4 ⇒ y = 5 4 - x vì y > 0 ⇒ 0 < x < 5 4 ⇒ S = 4 x + 1 5 - 4 x ∀ x ∈ 0 ; 5 4
Xét f ( x ) = 4 x - 1 5 - 4 x
f ' ( x ) = 0 ⇔ - 4 x 2 + 4 5 - 4 x 2 = 0 ⇒ x = 1 ∈ 0 ; 5 4
Bảng biến thiên:
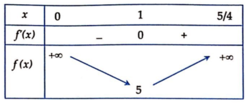
⇒ m i n S = m i n 0 ; 5 4 f ( x ) = 5 khi x = 1 y = 1 ⇒ a . b = 1 4

TK: Tìm Min (x^4 + 1) (y^4 + 1) với x + y = căn10 ; x , y > 0 - Thanh Truc

ta có x+y=\(\sqrt{10}\)=>(x+y)^2=10
A=(x^4+1)(y^4+1)
=x^4.y^4+1+x^4+y^4+2x^2.y^2-2x^2.y^2
=x^4.y^4+1+(x^2+y^2)^2-2x^y^2=x^4.y^4+1+[(x+y)^2-2xy]
=x^4.y^4+1+(10-2xy)-2x^2.y^2
=x^4.y^4+1+100-40xy+4.x^2.y^2-2x^2.y^2
=x^4.y^4+101-40xy+2.x^2.y^2
=(x^4.y^4-8.x^2.y^2+16)+(10.x^2.y^2-40xy+40)+45
=(x^2.y^2-4)^2+10.(xy-2)^2+45\(\ge\)0
dấu = xảy ra \(\Leftrightarrow\)\(\left\{{}\begin{matrix}x+y=\sqrt{10}\\x.y=2\end{matrix}\right.\)
vậy Min A=45
\(\left\{{}\begin{matrix}x+y=\sqrt{10}\\x.y=2\end{matrix}\right.\)là nghiệm pt x^2-\(\sqrt{10}\)x+2
=>\(\Delta\)=(-\(\sqrt{10}\))^2-4.2=2>0
=>\(\left\{{}\begin{matrix}x=\dfrac{\sqrt{10}-\sqrt{2}}{2}\\y=\dfrac{\sqrt{10}+\sqrt{2}}{2}\end{matrix}\right.\)hoặc \(\left\{{}\begin{matrix}x=\dfrac{\sqrt{10}-\sqrt{2}}{2}\\y=\dfrac{\sqrt{10}+\sqrt{2}}{2}\end{matrix}\right.\)

Có \(P=\dfrac{x+z}{xyz}=\dfrac{1}{yz}+\dfrac{1}{xy}=\dfrac{1}{y}\left(\dfrac{1}{x}+\dfrac{1}{z}\right)\ge\dfrac{1}{y}.\dfrac{4}{x+z}\)
\(=\dfrac{4}{y\left(x+z\right)}=\dfrac{4}{y\left(4-y\right)}=\dfrac{4}{-y^2+4y}=\dfrac{4}{-\left(y-2\right)^2+4}\ge1\)
"=" xảy ra khi y = 2 ; x = 1 ; z = 1

Bạn kiểm tra lại đề bài, với biểu thức thế này thì không thể tìm được điểm rơi (nó là nghiệm của 1 pt bậc 4 hệ số rất xấu ko thể giải được)

\(P=\left(x^4+1\right)\left(y^4+1\right)=x^4y^4+x^4+y^4+1\)
Ta có \(x^2+y^2=\left(x+y\right)^2-2xy=10-2xy\)
\(\Rightarrow x^4+y^4=\left(x^2+y^2\right)^2-2x^2y^2=\left(10-2xy\right)^2-2x^2y^2=100-40xy+2x^2y^2\)
\(\Rightarrow P=\left(xy\right)^4+101-40xy+2x^2y^2\)
\(=\left[\left(xy\right)^4-8\left(xy\right)^2+16\right]+10\left[\left(xy\right)^2-4xy+4\right]+45\)
\(=\left(x^2y^2-4\right)^2+10\left(xy-2\right)^2+45\)
\(\Rightarrow P\ge45\)
Dấu "=" xảy ra khi xy=2
Lại có \(x+y=\sqrt{10}\)
\(\Rightarrow x=\sqrt{10}-y\Rightarrow xy=\sqrt{10}y-y^2=2\)
\(\Rightarrow y^2-\sqrt{10y}+2=0\)
Ta có \(\Delta=10-8=2\)
\(\Rightarrow y=\frac{\sqrt{10}+\sqrt{2}}{2}\)
\(\Rightarrow x=\frac{4}{\sqrt{10}+\sqrt{2}}=\frac{\sqrt{10}-\sqrt{2}}{2}\)
Vậy giá trị nhỏ nhất của P là 45 khi \(\hept{\begin{cases}x=\frac{\sqrt{10}-\sqrt{2}}{2}\\y=\frac{\sqrt{10}+\sqrt{2}}{2}\end{cases}}\)