Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh 2a, tam giác SAB vuông cân tại S, tam giác SCD đều thì thể tích khối S.ABCD là:
A. 4 a 3 3 3
B. 4 a 3 3
C. 2 a 3 3
D. 2 a 3 3 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


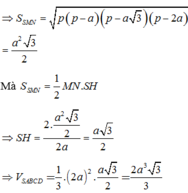

Đáp án D.
Gọi M, N lần lượt là trung điểm của AB và CD
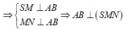
![]()
Gọi H là hình chiếu của S lên MN => SH ⊥ (ABCD)
Ta có ![]()
![]()
![]()
![]()
Mà ![]()
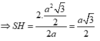
![]()

Đáp án D
Gọi M, N lần lượt là trung điểm của AB và CD
⇒ S M ⊥ A B M N ⊥ A B ⇒ A B ⊥ S M N ⇒ ( A B C D ) ⊥ ( S M N )
Gọi H là hình chiếu của S lên M N ⇒ S H ⊥ A B C D
Ta có S M = 1 2 A B = a , S N = 2 a . 3 2 = a 3 , M N = 2 a
⇒ S S M N = p ( p - a ) ( p - a 3 ) ( p - 2 a ) = a 2 3 2
Mà S S M N = 1 2 M N . S H ⇒ S H = 2 . a 2 3 2 2 a = a 3 2
⇒ V S . A B C D = 1 3 . 2 a 2 . a 3 2 = 2 a 3 3 3