Cho tam giác ABC có hai đường cao AK và BH cắt nhau tại I, biết
∠ A = 60 o , ∠ B = 70 o
b. Tính góc (AIB)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

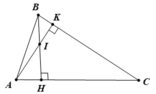
b. Trong tam giác vuông ABH có ∠(ABH) + ∠(AHB) + ∠(BAH) = 180o
Nên ∠(ABH) = 180o - 60o - 90o = 30o ( 1 điểm)
Trong tam giác vuông ABK có (BAK) + (ABK) + (BKA) = 180o
Nên ∠(BAH) = 180o - 70o - 90o = 20o ( 1 điểm)
Trong tam giác ABM có ∠(ABI) + ∠(BAI) + ∠(IAB) = 180onên
∠(AMB) = 180o - 20o - 30o = 130o ( 1 điểm)

a: góc BIH+góc BKH=180 độ
=>BIHK nội tiếp
b: OE vuông góc BC
=>sđ cung EB=sđ cung EC
=>góc BAE=góc CAE
Xét ΔAKB vuông tại K và ΔACF vuông tại C có
góc ABK=góc AFC
=>ΔAKB đồng dạng với ΔACF
=>góc BAK=góc CAF
=>góc DAE=góc FAE
=>AE là phân giác của góc DAF

a. Hình vẽ ( 1 điểm)
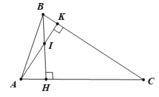
Vì ∠A = 60o,B = 70o nên ∠C = 180o - 60o - 70o = 50o ( 1 điểm)
Vì C < A < B ⇒ AB < BC < AC ( 1 điểm)

a. Hình vẽ ( 1 điểm)

Vì ∠A = 60o,B = 70o nên ∠C = 180o - 60o - 70o = 50o ( 1 điểm)
Vì C < A < B ⇒ AB < BC < AC ( 1 điểm)

a) Nối HK; BK; CK
+) Góc ACK ; góc ABK là góc nội tiếp chắn nửa đường tròn (O;R) => góc ACK = 90o ; góc ABK = 90o
=> AB | BK; AC | CK
Mà AB | CF; AC | BE nên CF // BK ; BE // CK => T/g BHCK là hình bình hành => 2 đường chéo BC ; HK cắt nhau tại trung điểm của mỗi đường
Mà I là trung điểm của BC => I là trung điểm của HK
+) Xét tam giác AKH có: O; I là trung điểm của AK; HK => OI là đường trung bình của tam giác AKH => AH = 2.OI
b) +) Góc BAC là nội tiếp chắn cung BC => Góc BAC = 1/2 góc BOC ( Mối liên hệ giữa góc ở tâm và góc nội tiếp)
=> góc BOC = 2.60o = 120o . Mà tam giác BOC cân tại O ; OI là đường trung tuyến nên đồng thời là đường p/g và đường cao
=> góc BOI = 1/2 góc BOC = 60o
+) Xét tam giác vuông BIO có: BI = OB.sin BOI = R. sin 60o = \(\frac{R\sqrt{3}}{2}\) => BC = 2.BI = \(R\sqrt{3}\)
Vậy....

+) Góc xAC = góc ABC + ACB (tính chất góc ngoài tam giác)
góc A2 = xAC / 2
=> góc A2 = (góc ABC + C1) / 2 = B1 + ( C1 / 2 ) (Vì góc B1 = ABC /2 )
+) Trong tam giác AIB: góc AIB = 180o - (B1 + A1 + A2)
= 180o - (B1 + A1 +B1 + ( C1 / 2 ) )
= 180o - (2.B1 + A1 + ( C1 / 2 ) )
= 180o - (B + A1 + ( C1 / 2 ))
Mà B + A1 = 180o - C1 = 180o - 70o = 110o; C1 / 2 = 70o/ 2 = 35o
=> góc AIB = 180o - (110o + 35o) = 180o - 145o = 35o

1. \(3x-15=2x\left(x-5\right)\)
\(\Leftrightarrow3\left(x-5\right)-2x\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right).\left(3-2x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-5=0\\3-2x=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=5\\x=\frac{3}{2}\end{cases}}\)
Vậy \(S=\left\{5;\frac{3}{2}\right\}\)
a. Xét \(\Delta ABC\)và \(\Delta HAC\)có:
Góc C: chung (gt)
Góc HAC = Góc ABC ( cùng phụ với góc ACB)
\(\Rightarrow\Delta ABC\infty\Delta HAC\)
b.Ta có: \(\Delta ABC\infty\Delta HAC\)(cmt)
\(\Rightarrow\frac{BC}{AC}=\frac{AC}{HC}\Rightarrow AC^2=BC.HC=\left(BH+HC\right).HC=\left(9+12\right).12=252cm.\Rightarrow AC=\sqrt{252}=6\sqrt{7}\)
b. Trong tam giác vuông ABH có ∠(ABH) + ∠(AHB) + ∠(BAH) = 180o
Nên ∠(ABH) = 180o - 60o - 90o = 30o ( 1 điểm)
Trong tam giác vuông ABK có (BAK) + (ABK) + (BKA) = 180o
Nên ∠(BAH) = 180o - 70o - 90o = 20o ( 1 điểm)
Trong tam giác ABM có ∠(ABI) + ∠(BAI) + ∠(IAB) = 180onên
∠(AMB) = 180o - 20o - 30o = 130o ( 1 điểm)