Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Tại t = 0 x = 2 , 5 2 v < 0 ; T = s
Lực kéo về triệt tiêu khi qua VTCB
Kể từ t=0, thời điểm lực kéo về triệt tiêu lần thứ ba: t = T 8 + T = 2 , 25 s
Đáp án C
+ Tại t = 0 vật đi qua vị trí x = + 2 2 theo chiều âm. Lực kéo về của vật bị triệt tiêu khi vật đi qua vị trí cân bằng.
→ Tổng thời gian để lực kéo về triệt tiêu lần thứ ba là
Đáp án C
+ Lực kéo về triệt tiêu khi qua VTCB
+ Kể từ , thời điểm lực kéo về triệt tiêu lần thứ ba:
Mỗi câu hỏi bạn nên hỏi 1 bài thôi để tiện trao đổi nhé.
Biểu diễn dao động bằng véc tơ quay ta có:
Để vật qua li độ 1 cm theo chiều dương thì véc tơ quay qua N.
Trong giây đầu tiên, véc tơ quay đã quay 1 góc là: \(5\pi\), ứng với 2,5 vòng quay.
Xuất phát từ M ta thấy véc tơ quay quay đc 2,5 vòng thì nó qua N 3 lần do vậy trong giây đầu tiên, vật qua li độ 1cm theo chiều dương 3 lần.
Bạn xem thêm lí thuyết phần này ở đây nhé
Phương pháp véc tơ quay và ứng dụng | Học trực tuyến
Bài 1 :
T = 2π / ω = 0.4 s
Vật thực hiện được 2 chu kì và chuyển động thêm trong 0.2 s (T/2 ) nữa
1 chu kì vật qua vị trí có li độ x=2cm theo chiều dương được "1 " lần
⇒ 2 ________________________________________... lần
phần lẻ 0.2s (T/2) , (góc quét là π ) (tức là chất điểm CĐ tròn đều đến vị trí ban đầu và góc bán kính quét thêm π (rad) nữa, vị trí lúc nầy:
x = 1 + 2cos(-π/2 + π ) = 1, (vận tốc dương) vật qua vị trí có li độ x=2cm theo chiều dương thêm 1 lần nữa
(từ VT ban đầu (vị tri +1 cm ) –> biên dương , về vị trí có ly độ x = +1 cm
do đó trong giây đầu tiên kể từ lúc t=0 vật qua vị trí có li độ x=2cm theo chiều dương được 3 lần
Chọn A
Từ pt \(v=16\pi\cos\left(4\pi t-\dfrac{\pi}{6}\right)=16\pi\cos\left(4\pi t-\dfrac{2\pi}{3}+\dfrac{\pi}{2}\right)\) (cm/s), ta suy ra \(\omega=4\pi\left(rad/s\right)\), lại có \(\omega A=16\pi\Leftrightarrow A=\dfrac{16\pi}{\omega}=4\left(cm\right)\)
\(\varphi_0=-\dfrac{2\pi}{3}\); \(T=\dfrac{2\pi}{\omega}=0,5\left(s\right)\)
Đường tròn lượng giác:
Từ đây, ta có thể thấy tại thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ khi dao động, góc quét của vật là \(\Delta\varphi=\dfrac{\pi}{3}+1011.2\pi=\dfrac{6067}{3}\pi\) (rad)
Thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ lúc bắt đầu dao động là \(\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{6067}{3}\pi}{2\pi}.0,5=\dfrac{6067}{12}\approx505,58\left(s\right)\)
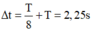
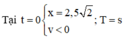
Chọn A.
Lực hồi phục luôn luôn hướng về VTCB, lực hồi phục sinh công dương khi vật chuyển động về VTCB và sinh công âm khi vật chuyển động ra VT biên.
Trong một chu kì, một nửa thời gian (T/2) lực hồi phục sinh công âm một nửa thời gian (T/2) sinh công dương.
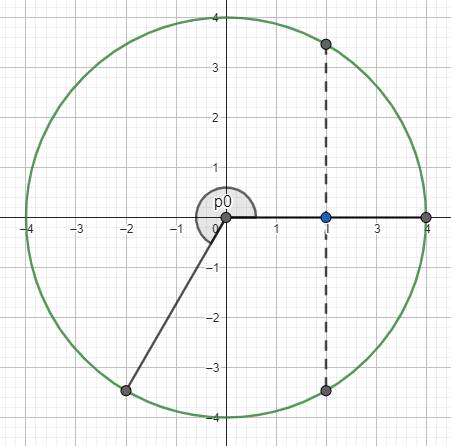
Dừa vào VTLG ta xác định được:
Lần 1, vật qua li độ x = -10 cm theo chiều âm ứng với góc quét từ đến . Trong gia đoạn này khoảng thời gian sinh công dương là T/4 (ứng với phần gạch chéo).
Để đến thời điểm lần thứ 2017, vật qua li độ x = -10 cm theo chiều âm thì cần quét thêm 2016 vòng và thời gian sinh công dương có thêm là 2016.T/2=1008T
Tổng thời gian: T/4 + 1008T = 1209.9 s.