Phần tự luận
Nội dung câu hỏi 1
a) Vẽ đồ thị của hàm số y = -1/2 (P)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Với x = 0 ⇒ y = 4
⇒ Đồ thị hàm số cắt trục tung tại điểm B (0; 4)
Với y = 0 ⇒ x = -4
⇒ Đồ thị hàm số cắt trục hoành tại điểm A (-4; 0)
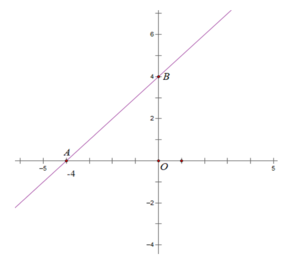
Đường thẳng AB chính là đồ thị hàm số y = x + 4

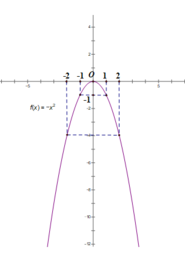
a) Lập bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y = - x 2 | -4 | -1 | 0 | -1 | -4 |
Đồ thị hàm số y = - x 2 là một đường parabol nằm phía dưới trục hoành, nhận trục Oy làm trục đối xứng, nhận gốc O (0; 0) làm đỉnh và là điểm cao nhất.

a) Vì đồ thị hàm số y = a x 2 đi qua điểm A(-2; 2) nên ta có:
2 = a. 2 2 ⇒ 4a = 2 ⇒ a = 1/2
⇒ Hàm số cần tìm là y = 1/2 x 2

Câu 1:
a: Khi x=4 thì \(P=\sqrt{49\cdot4}-\sqrt{16\cdot4}+\sqrt{25\cdot4}-1=7\cdot2-8\cdot2+5\cdot2-1=7\)
b: \(P=7\sqrt{x}-4\sqrt{x}+5\sqrt{x}-1=8\sqrt{x}-1\)

\(a,m=3\Leftrightarrow y=f\left(x\right)=x+2\)
\(b,\) PT giao Ox: \(y=0\Leftrightarrow x=-2\Leftrightarrow A\left(-2;0\right)\Leftrightarrow OA=2\)
PT giao Oy: \(x=0\Leftrightarrow y=2\Leftrightarrow B\left(0;2\right)\Leftrightarrow OB=2\)
Vậy \(S_{AOB}=\dfrac{1}{2}OA\cdot OB=\dfrac{1}{2}\cdot2\cdot2=2\left(đvdt\right)\)

b, Phương trình hoành độ giao điểm:
\(\Rightarrow2x^2=x+3\)
\(\Leftrightarrow2x^2-x-3=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{2}\end{matrix}\right.\)
\(x=-1\Rightarrow y=2\Rightarrow\left(-1;2\right)\)
\(x=\dfrac{3}{2}\Rightarrow y=\dfrac{9}{2}\Rightarrow\left(\dfrac{3}{2};\dfrac{9}{2}\right)\)
a) Vẽ đồ thị hàm số (P): y = (-1)/2 x 2
Bảng giá trị :
Đồ thị hàm số y = (-1)/2 x 2 là một đường Parabol nằm phía dưới trục hoành, nhận trục tung làm trục đối xứng, nhận gôc tọa độ O(0;0) làm đỉnh và là điểm cao nhất.